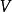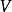格爾斯滕哈伯代數是Gerstenhaber在研究結合代數的形變時發現的。一個結合代數的形變跟它的Hochschild上復形有密切的關係，Gerstenhaber證明，Hochschild上復形實際上形成一個微分分次李代數，並且這個微分分次李代數完全控制了該結合代數的形變。Gerstenhaber的研究受到小平邦彥（Kodaira）-Spencer關於流形復結構形變研究的啟發，這些思想後來由Deligne和Kontsevich等人加以系統完成。
基本介紹
- 中文名：格爾斯滕哈伯代數
- 外文名：Gerstenhaber algebra
- 分類：數理科學
定義,歷史,例子,參見,
定義
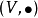
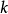
李括弧對其兩個變元都是乘積
的導子，即對任給
，
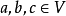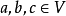
有些文獻也把格爾斯滕哈伯代數稱為辮代數（braid algebra）。
歷史
在下面後4個例子中，例2和例3是1990年代之前發現的，1993年，Deligne在給一些數學家的通信中猜測它們之間也許是有關係的，用數學語言表述，即：對任何一個結合代數，其Hochschild上復形是little disks operad的鏈(chain) operad上的代數。這就是著名的Deligne猜想，最後由Kontsevich-Soibelman，McClure-Smith，Tamarkin和Voronov等人解決。Deligne猜想的證明涉及到了很多高深的數學工具，而這些工具都與拓撲共形場論有著密切的聯繫，因而引起了很多人的興趣。
稍後，在1997年，Chas和Sullivan的研究論文發表了名為弦拓撲的論文，發現了例5。他們的研究結果引起了數學家們很大的關注和進一步的研究，從而開闢了一門嶄新的學科。
最後，需要補充的是，關於Gerstenhaber代數的研究往往伴隨著Batalin-Vilkovisky代數（簡稱BV代數）的研究。BV代數是一類特殊的Gerstenhaber代數，往往由Gerstenhaber代數裡面的某種對稱性而得到。
例子
下面是一些Gerstenhaber代數的例子，因為構造都比較複雜，因此只列出結果，有興趣的讀者可以參考所給文獻資料：
設
是一個李代數，記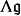
為其所對應的鏈復形，則在其上有一個自然的Gerstenhaber代數結構，乘法由外積給出，李括弧為從
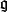上誘導的李括弧給出（這是一個比較平凡的例子，因此一般人並不重點討論，但它在構造Gerstenhaber代數的同倫論中非常重要）；
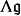
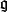
設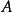
是數域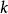
上的結合代數，Gerstenhaber證明：
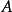的霍赫希爾德上同調形成一個Gerstenhaber代數；
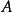
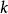
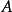
記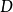
為little disks operad，Cohen證明：
的同調群形成一個Gerstenhaber代數；
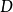
Lian和Zuckerman證明了，在弦理論的背景（background，指從弦理論裡面抽象出來的代數結構）中，存在一個Gerstenhaber代數結構；
設
是一個緊緻光滑的流形，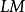
是它的自由環路空間（free loop space）。Chas和Sullivan證明：
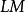的同調群形成一個Gerstenhaber代數。
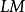
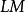
參見
- Batalin-Vilkovisky代數
