復二次超曲面

復二次超曲面(complex quadric)是復射影空間中的特殊超曲面。復射影空間是實射影空間在復情形的推廣，是一種典型的複流形。特別地，當n=1時，P(C)是普通2維球面S的複數表示，稱為黎曼球面。

基本介紹

• 中文名：復二次超曲面
• 外文名：complex quadric
• 領域 ：數學
• 學科：整體幾何
• 性質：特殊超曲面
• 本質：代數流形

概念

復二次超曲面(complex quadric)是復射影空間中的特殊超曲面。復射影空間CP^m中齊次坐標z⁰，z¹，…，z^m滿足方程：

的代數流形，稱為復二次超曲面。

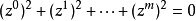
復射影空間

實射影空間在復情形的推廣，是一種典型的複流形。設

為n+1維復空間，把Cⁿ⁺¹中每一條過原點的復直線等同於一個點，便得復n維射影空間Pⁿ(C)。另一方面，Cⁿ⁺¹\{0}中的兩個點(z₁，z₂，…，z_n+1)，(z′₁，z′₂，…，z′_n+1)稱為等價的，如果(z′₁，z′₂，…，z′_n+1)=λ(z₁，z₂，…，z_n+1)，其中λ為一個非零複數。顯然，這是一個等價關係，記此關係之下，含點(z₁，z₂，…，z_n+1)的等價類為[z₁，z₂，…，z_n+1]，則Pⁿ(C)便是一切[z₁，z₂，…，z_n+1]之集合，令：

則這是一個商映射，P(C)具有這個商映射之下的商拓撲。容易證明，P(C)在自然結構之下，成為緊連通複流形。特別地，當n=1時，P(C)是普通2維球面S的複數表示，稱為黎曼球面。

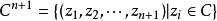
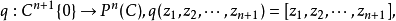
射影空間

整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形)，為方便起見引入無窮遠點的概念，即規定平面上每條直線上有一個無窮遠點，兩條直線平行就是相交於無窮遠點，所有無窮遠點組成一條無窮遠直線。這種構造方法還可以推廣到高維空間，建立n維(實)射影空間P_R。在n維射影空間中常採用齊次坐標(X₀∶X₁∶…∶X_n)，其中X₀，X₁，…，X_n不全為0；若a≠0，則(aX₀∶aX₁∶…∶aX_n)與(X₀∶X₁∶…∶X_n)表示同一個點。因此n維(實)射影空間同構於(R-{0})/R。進一步的研究表明P_R是緊緻解析流形。若令U_i(0≤i≤n)為P_R中坐標X_i≠0的點全體，則U_iR，且U₀，U₁，…，U_n組成Pⁿ_R的一個開覆蓋。上述構造方法可以推廣到任意體K上，建立K上的n維射影空間P_K。在概形理論中，還將射影空間建立在整數環Z上，即建立射影概形P_Z。由此對任意概形X可以建立Pⁿ_X，它是X和Pⁿ_Z(在Spec Z上)的纖維積。特別地，若X=Spec K(K為域)，則Pⁿ_X=Pⁿ_K。

由於射影空間的性質非常豐富難以全面列舉，僅舉數例如下：

1.P¹_R同胚於圓，P¹_C可看做添上無窮遠點的複平面，同胚於球面。

2.P²_R是單側曲面，可以同胚地嵌入四維空間R⁴，但不能同胚地嵌入三維空間R³，P²_C是代數極小曲面。

3.Pⁿ_C是克勒流形，它的閉解析子空間都是代數的。

4.對任意域k，Pⁿ_k是齊性空間，其切叢由整體向量場生成，其自同構群為射影群PSL(n+1，k)，其皮卡群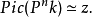

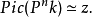
代數流形

代數流形是復射影空間中的代數子集。若P(C)的一個子流形是P(C)的一個代數子集，則稱這個復子流形為代數子流形。若一個複流形是雙全純於某個復射影空間的一個代數子流形，也稱這個複流形為代數流形。

子流形

設N，M分別為n，m維的微分流形。F為N到M的C映射。若F的秩(rankF)在N的每點都等於n，則稱映射F為N到M的一個浸入。若浸入F是單射，則稱F為1-1浸入。

設F為N到M的1-1浸入，此映射下的像Ñ=F(N)⊂M，在Ñ上賦予拓撲和微分結構：設(U，ᵠ)為N的坐標鄰域，令V=F(U)，=ᵠ°F，則(V，)為Ñ上的坐標鄰域。使得F成為N到Ñ的微分同胚，則Ñ稱為M的n維浸入子流形。

設F為N到M的1-1浸入，若F同時是N到M內的同胚映射，亦即，在映射的像Ñ=F(N)取M中的子空間拓撲時，F是N到Ñ上的同胚映射。則稱Ñ為M的n維嵌入子流形。映射F稱為嵌入映射。

浸入和嵌入的區別是就整體而言，在局部二者是一致的。事實上，若F為N到M的浸入映射，則在任何點P∈N，總存在P的坐標鄰域 (U，)，使得F限制在U上F|u是U到M內的嵌入。

設N是微分流形M的子集，具有以下性質：N的每點P，存在包含P的M中的坐標鄰域(U，ᵠ)其局部坐標為x，…，x，使得： (1)(p)=(0，…，0) ∈R。(2) (U)=C_ε(0)——以原點為中心的立方體鄰域。(3) ᵠ(U∩N) = {x∈C^m_ε(0)|xⁿ⁺¹=…=x^m=0}。具有如上性質的子集N稱M的n維正則子流形，正則子流形本質上就是嵌入子流形。

複流形

區圖中映射是映到復空間的流形.設M是一個仿緊豪斯多夫拓撲空間，若在M上存在一個圖冊A={(U_i，φ_i)|i∈I}，滿足下列條件，則稱A是M的一個n維複流形結構，M為復n維流形，或n維複流形：

1.對所有的i∈I，φ_i是U_i到Cⁿ的開子集φ_i(U_i)上的一個同胚；

2.對於任意的i，j∈I，當U_i∩U_j≠∅時，φ_i°φ^-1_j|_φj(U_i∩U_j)：φ_j(U_i∩U_j)→φ_i(U_i∩U_j)是一個雙全純映射。

此處通常總認為圖冊A是最大的.即若(U，φ)是M的任一個區圖且φ°φ^-1_j是雙全純的，則(U，φ)∈A。容易證明，每個n維複流形有2n維實解析流形的結構，作為實解析流形是可定向的而且具有一個由復結構決定的特定的定向。