基本介紹
- 中文名:齊性空間
- 外文名:homogeneous space
- 別稱:齊性流形
- 領域:數學
- 含義:容有可遷變換群的微分流形
理論介紹
定義



例子


陪集定理





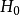


準齊性質
物理原理
















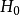








齊性空間,又稱齊性流形,是容有可遷變換群的微分流形。齊性空間理論與李群論有極為密切的聯繫。在幾何中出現的許多重要流形都是齊性空間。齊性空間在現代數學...
兩點齊性空lei (two-point homogeneous space)一類簡單的齊性空間.若對於黎曼流形M中任何兩個距離相等的點對p,、與p., q.,(即d<q,p)=d
半單李群等也是黎曼對稱空間.由於保持了對稱性,自然就保持了空間每點都處於平等地位的勻齊性,也就是說黎曼對稱空間M是齊性空間,即M的等距變換群是可遞地作用於...
在拓撲結構中,拓撲空間被稱為簡單連線(或單連通),如果它是路徑連線的,並且兩點之間的每條路徑都可以連續變換,停留在空間內其他這樣的路徑,同時保留有問題的兩個...
4.對任意域k,Pk是齊性空間,其切叢由整體向量場生成,其自同構群為射影群PSL(n+1,k),其皮卡群Pic(Pnk)Z。射影空間微分結構微分流形 編輯 ...
E.嘉當(Cartan)引進了埃爾米特(Hermite)對稱空間,從齊性空間的角度給出了完全分類,證明了它是四大類典型域(可以在復歐氏空間中明確定義)和兩個例外的不可分解...
的領袖”(陳省身語).嚴志達把李群的表示理論用於研究李群與齊性空間的拓撲性質,從而算出了特殊單李群的Betti數與一些齊性空間的Betti數.這是很有創見的歷史性的...
積分幾何的研究從二維歐幾里得平面、三維歐幾里得空間開始,逐步拓廣到高維歐幾里得空間和非歐幾里得空間,然後概括為滿足一定條件的齊性空間。...
該專著指導和培養了國內一大批數學工作者繼續這一方向的研究,他們套用龔升在酉群的調和分析中建立的思想和方法,研究緊李群上的調和分析,之後又研究緊緻齊性空間上...
谷超豪主要從事偏微分方程、微分幾何、數學物理等方面的研究和教學工作,在一般空間微分幾何學、齊性黎曼空間、無限維變換擬群、雙曲型和混合型偏微分方程、規範場理論...
是G/H上關於G的左作用不變的n形式,則稱之為齊性空間G/H上的不變密度,記為d<G/H).當H為G的閉正規子群時,齊性空間G/H上必存在不變密度.[1] ...
以李群作用的齊性空間和代數流形的豐富實例為模板,研究緊凱萊流形的幾何拓撲性質。最近對有對稱結構即帶群作用的凱萊流形、Fano流形尤其是低維凱萊流形的幾何拓撲...
2005-11 上海大學理學院數學系 齊性空間的積分幾何學。2012-06 復旦大學 On the Alexandrov-Fenchel inequality。2005-12 陳省身數學研究所 Kinematic formulas in...
4.對任意域k,Pk是齊性空間,其切叢由整體向量場生成,其自同構群為射影群PSL(n+1,k),其皮卡群Pic(Pk)Z。射影態射射影簇 編輯 設P(E)為由向量空間E...
1 19世紀幾何中的問題 2 齊性空間 3 例子:仿射幾何 4 在後來的工作上的影響 5 從愛爾蘭根綱領的抽象的回歸 6 克萊因幾何的推廣 愛爾蘭...
塞爾伯格跡公式是數學中非交換調和分析的重要定理之一。此公式表達了齊性空間 G/ Γ 的函式空間上某類運算元的跡數,其中G是李群而Γ是其離散子群。又數學家...
在李群及齊性空間、覆蓋空間及一般的向量叢等數學方向上都有套用。纖維叢理論來源 編輯 1946年美國的斯丁路特、美籍華人陳省身、法國的艾勒斯曼共同提出纖維叢的...
積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括到滿足一定條件的齊性空間。中文名 積分幾何學 對象 積分考察圖 屬性 幾何...
先後多次參加國際國內會議,2011年在中科院數學所參加代數幾何與復幾何國際會議;2012年在北京參加整點與齊性空間的國際會議;2013年8月,2016年5月分別在長春及揚州...
單李群齊性空間中的相交理論。北京大學學報(自然科學版)35(3), pp 297--301, 1999無。自由群外自同構群中子群的階。北京大學博士學位論文, 1999無。...
3.6齊性空間 3.6.1Lie群和不變度量 3.6.2齊性空間 3.6.3對稱空間 3.7主叢及其聯絡 3.8Gauss—Bonnet—Chern公式 3.8.1向量場的指標 3.8.2單位球...
若我們有一個主叢P其底空間是空間或時空而結構群是一個李群,則P的截面組成一個規範變換群的主齊性空間。我們可以在該主叢上定義一個聯絡(規範聯絡),這可以在...
侯自新教授多年從事李群、李代數及齊性空間微分幾何等方面的研究與教學工作。研究解決了一些長期未能解決的數學問題,如:明確給出了實半單李代數的Weyl群的結構,完...
本書的主要內容是:微分流形、示性類理論、表示論大意、Hodge理論、Hirzebruch...參考文獻第15章 示性類緒論15.1 Borel-Hirzebruch格式15.2 齊性空間上的計算...
陳省身則在諸如文獻[5,6]的工作中,表明了如何把 運動學公式推廣到齊性空間。 ²布拉施克也按照克萊因的埃朗根綱領,開創了仿射微分幾何學的研究。在其關於微分...
與愛爾蘭根綱領一致,閔可夫斯基空間的幾何由龐加萊群所規定的:閔可夫斯基空間可被視為龐加萊群的齊性空間。龐加萊代數是龐加萊群的李代數。更具體的來說,正式...
4、《齊性空間上的最大函式及J-N定理》,自然雜誌,1984年6月5、《中國教育積體電路(IC)卡規範》,東方出版社,2002年王鍵學術成果 編輯 ...
