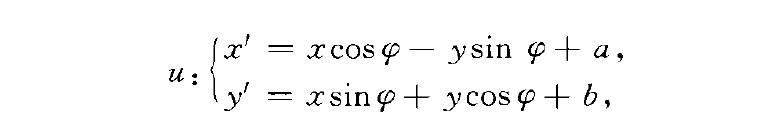
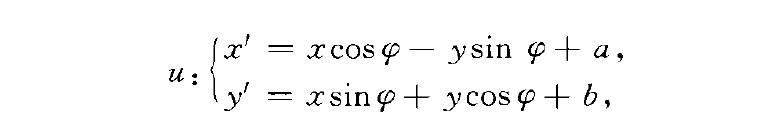
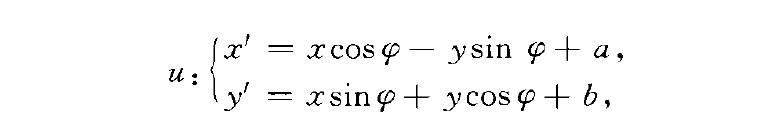
不變密度(invariant density)積分幾何中各種密度的統稱.指某一可遷變換群下不變的微分形式.在R'中,設有動點P(二,y)和動直線G:二cos }p-}ysin}p-}=0,分...
根據密度公式的變形式:m=Vρ或 V=m/ρ,可以計算出物體的質量和體積,特別是一些質量和體積不便直接測量的問題,如計算不規則形狀物體的體積、紀念碑的質量等。 4...
在顯示地震磁帶記錄時,使記錄在照相紙上感光的密度和地震波的振幅成正比,故稱變密度記錄。...
“密度變化”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
體積密度是一個漢語辭彙,表示材料在包含實體積。在建築材料中,對材料的質量和體積之比稱為密度。在不同構造狀態下又可分為真密度、表觀密度和堆積密度,而表觀...
聲波變密度測井屬於聲波測井的一種,其原理是利用水泥和泥漿(或水)其聲阻抗的較大差異對沿套管軸向傳播的聲波的衰減影響來反映水泥與套管間、套管與地層的膠結質量...
年輪密度測定是樹木年輪氣候學的研究方法之一。由於樹木年輪不僅在寬度上有逐年變化,而且密度亦有顯著差異,同時與氣候變化關係十分密切,因此自20世紀70年代以來,測定...
SF6斷路器中的SF6氣體是密封在一個固定不變的容器內的,在20℃時的額定壓力下,它具有一定的密度值,在斷路器運行的各種允許條件範圍內,儘管SF6氣體的壓力隨著溫度...
指因病毒粒子中所含有的核酸量的增減而引起病毒粒子的飄浮密度發生變化的突變株。λ,T7等噬菌體DNA發生部分缺失而變短時,若缺失部分不含有必不可少的信息,則也...
保險密度是指按限定的統計區域內常住人口平均保險費的數額。它標誌著該地區保險業務的發展程度,也反映了該地區經濟發展的狀況與人們保險意識的強弱。...
又稱磁通密度。設磁場中某點有正電荷q,它的速度是v,磁場對它的作用力是F;改變速度v的方向但維持其量值不變,直到力的量值F為最大;定義該點的磁感應強度B的...
速度-密度曲線(speed-density curve)是指表示交通流的速度v與密度K之間相互關係的曲線。車流速度隨車流密度的增加而降低,當密度達到最大值(即隊塞密度)時,車流...
具滲透性產品的密度(Permeable Density) 所定義之體積含開放孔及封閉孔,粉末冶金中一般所稱之燒結密度即屬此,在精密陶瓷學中稱為體密度(Bulk Density)以下以 Db...
流量-密度曲線(flow-density curve)是指表示交通流量Q與密度K之間相互關係的曲線。密度過小(或大),流量均達不到最大值。只有當密度在某一合適值時,通過流量才...
流量-密度控制(volume-density control)是指考慮到延誤和各相累計交通量的交叉口...包括小時變化曲線(時變圖),日變化曲線(周變圖或口變圖)、月變化曲線(月變圖...
比重也稱相對密度,固體和液體的比重是該物質(完全密實狀態)的密度與在標準大氣壓,3.98℃時純H2O下的密度(999.972 kg/m3)的比值。氣體的比重是指該氣體的密度與...
因為液體的壓強等於密度、深度和重力加速度常數之積。在這個實驗中,水的密度不變,但深度一再增加,則下部的壓強越來越大,其液壓終於超過木桶能夠承受的上限,木桶...
型反應為正密度反應,即天敵的數量隨獵物數量的增加而增加;型反應, 型反應是無密度反應,即天敵的數量隨獵物數量的增加而保持不變;型...
物體的質量是永遠不變的。慣性之所以可以改變是因為慣性是保持質量場與質心相對關係的能力,而運動速度的增加與質量的增加都能夠產生同樣導致質量場密度變化的結果,所以...
