積分幾何數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。它起源於幾何機率的研究,其發展也始終與幾何機率相聯繫。積分幾何的研究從二維歐幾里得平面、三維歐幾里得空間開始,逐步拓廣到高維歐幾里得空間和非歐幾里得空間,然後概括為滿足一定條件的齊性空間。
基本介紹
- 中文名:積分幾何
- 外文名:integral geometry
- 屬性:本質上屬於整體微分幾何範疇
- 起源於:幾何機率的研究
簡介
基本信息












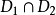
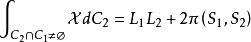
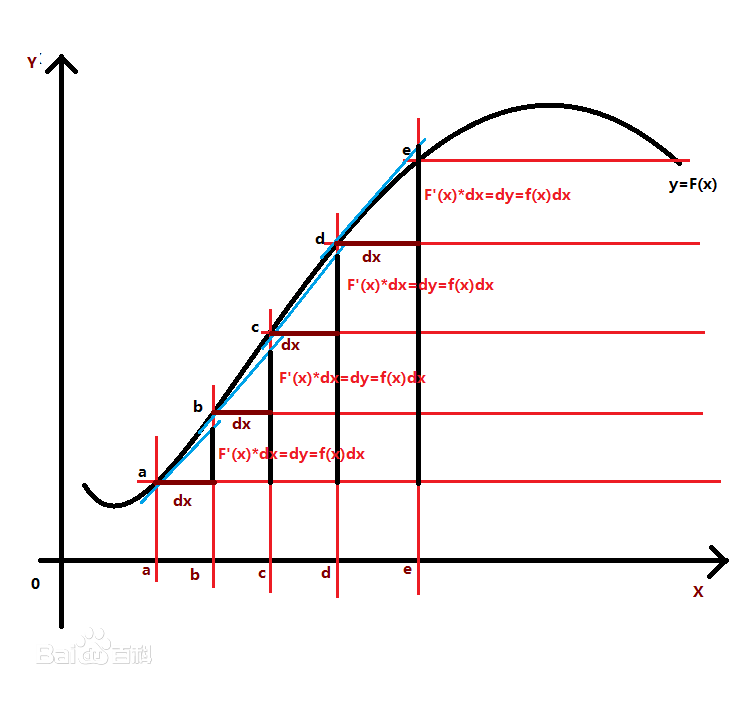
積分幾何數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。它起源於幾何機率的研究,其發展也始終與幾何機率相聯繫。積分幾何的研究從二維歐幾里得平面、三維歐幾里得空間開始,逐步拓廣到高維歐幾里得空間和非歐幾里得空間,然後概括為滿足一定條件的齊性空間。





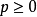

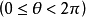
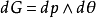

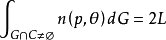





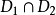
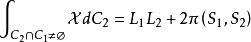
積分幾何數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。它起源於幾何機率的研究,其發展也始終與幾何機率相聯繫。積分幾何的研究從二維...
《積分幾何與幾何機率》是世界圖書出版公司出版的圖書,作者是(阿根廷)路易斯桑塔洛。...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
二重積分是二元函式在空間上的積分,同定積分類似,是某種特定形式的和的極限。本質是求曲頂柱體體積。重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心等...
微積分(Calculus),數學概念,是高等數學中研究函式的微分(Differentiation)、積分(Integration)以及有關概念和套用的數學分支。它是數學的一個基礎學科,內容主要包括極限...
幾何,就是研究空間結構及性質的一門學科。它是數學中最基本的研究內容之一,與分析、代數等等具有同樣重要的地位,並且關係極為密切。幾何學發展歷史悠長,內容豐富。...
高斯積分是在機率論和連續傅立葉變換等的統一化等計算中有廣泛的套用。在誤差函式的定義中它也出現。雖然誤差函式沒有初等函式,但是高斯積分可以通過微積分學的手段...
均質積分(quermass integral)亦稱平均截面測度.凸體論和積分幾何的重要概念.本質上是R"中凸集在((n-r)維平面上投影體積的積分平均值.若K為R"中的凸集,L。一...
幾何,就是研究空間結構及性質的一門學科。它是數學中最基本的研究內容之一,與分析、代數等等具有同樣重要的地位,並且關係極為密切。幾何學發展歷史悠長,內容豐富。...
英文Geometry一詞,是從希臘語演變而來的,其原意是土地測量、後被我國明朝的徐光啟翻譯成"幾何學"。依據大量實證研究,創造幾何學的是埃及人,幾何學因土地測量而...
勒貝格積分,是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是求其函式圖像與軸之間的面積。...
三重積分幾何意義 編輯 三重積分就是立體的質量。當積分函式為1時,就是其密度分布均勻且為1,質量就等於其體積值。當積分函式不為1時,說明密度分布不均勻。...
博赫納積分(Bochner integral)是按勒貝格積分方式定義的一種常用的向量值函式的積分。博赫納積分是勒貝格積分在向量值函式情形的直接推廣,是由博赫納(S.Bochner)在1932...
如果函式f(x,y)在有界閉區域D上連續,區域D的面積為S,且 m 和 M 分別是f(x,y)在D上的最小值和最大值,則mS ≤∫∫f(x,y)在D上的二重積分 ≤ MS...
無限維分析學的一個新分支。它起源於量子物理學中的連續積分和機率論中的隨機過程的樣本空間的研究。目前,泛函積分方法已深入到分理化量子場論、基本粒子理論、隨機...
積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括...
解析幾何指藉助笛卡爾坐標系,由笛卡爾、費馬等數學家創立並發展。它是利用解析式來研究幾何對象之間的關係和性質的一門幾何學分支,亦叫做坐標幾何。嚴格地講,解析...
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。...
