積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括到滿足一定條件的齊性空間。
基本介紹
- 中文名:積分幾何學
- 對象:積分考察圖
- 屬性:幾何範疇
- 對應:歐氏平面
簡介
基本信息
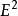
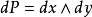
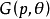
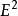










積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括到滿足一定條件的齊性空間。
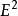


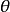


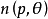
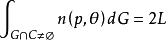
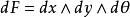




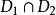

積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
積分學(integral calculus)數學分析的分支學科。即研究各種積分(理論、計算和套用)以及它們之間的關係的學科。積分學也是高等數學的基礎學科之一。積分學的研究對象...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
解析幾何指藉助笛卡爾坐標系,由笛卡爾、費馬等數學家創立並發展。它是利用解析式來研究幾何對象之間的關係和性質的一門幾何學分支,亦叫做坐標幾何。嚴格地講,解析...
積分幾何(integral geometry)數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。...
積分法 integral method; 是通過磁異常的積分運算求得磁性體產狀的定量解釋推斷...同時,還要求計算之前必須確定磁性體的幾何形狀,才能正確地選擇計算公式。...
博赫納積分是勒貝格積分在向量值函式情形的直接推廣,是由博赫納(S.Bochner)在1932年建立的,這種積分在向量值測度理論、運算元理論、機率論、隨機過程以及巴拿赫空間幾何...
光是一種電磁波,在物理學中,電磁波由電動力學中的麥克斯韋方程組描述;同時,光...圖1積分1.理想積分球原理理想積分球地條件:A、積分球地內表面為一完整地幾何...
不可分量幾何學(Ueometria indivisibilibus con一tinuorum nova quadam ratione promota ) 17世紀西方數學著作.直譯為《運用連續體的不可分量以新方式推進的幾何學...
從微積分成為一門學科來說,是在17世紀,但是積分的思想早在古代就已經產生了。...牛頓研究微積分著重於從運動學來考慮,萊布尼茨卻是側重於幾何學來考慮的。...
論文涉及的領域也十分廣泛,包括巴拿赫代數、調和分析、群表示論、積分幾何、廣義函式、無窮維李代數的上同調、微分方程、生物學和生理學。...
高斯積分是在機率論和連續傅立葉變換等的統一化等計算中有廣泛的套用。在誤差函式的定義中它也出現。雖然誤差函式沒有初等函式,但是高斯積分可以通過微積分學的手段...
無限維分析學的一個新分支。它起源於量子物理學中的連續積分和機率論中的隨機過程的樣本空間的研究。目前,泛函積分方法已深入到分理化量子場論、基本粒子理論、隨機...
均質積分(quermass integral)亦稱平均截面測度.凸體論和積分幾何的重要概念.本質上是R"中凸集在((n-r)維平面上投影體積的積分平均值.若K為R"中的凸集,L。一...
成為分析的“分水嶺”,人們常把勒貝格以前的分析學稱為經典分析,而把以由勒貝格...因此,在理論和套用上都迫切要求建立一種新的積分,它既能保持R積分的幾何直觀和...
二重積分幾何意義 在空間直角坐標系中,二重積分是各部分區域上柱體體積的代數和,在xoy平面上方的取正,在xoy平面下方的取負。某些特殊的被積函式f(x,y)的所表示...
(x,y)在D上的二重積分≤ MS這就是二重積分的估值定理 如果是一元函式f(x)...《關於曲面的一般研究》,全面系統的闡述了空間曲面的微分幾何學,並提出內蘊曲面...
