積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括到滿足一定條件的齊性空間。
基本介紹
- 中文名:積分幾何學
- 對象:積分考察圖
- 屬性:幾何範疇
- 對應:歐氏平面
簡介
基本信息





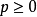

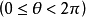
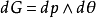

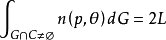





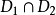
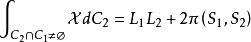

積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括到滿足一定條件的齊性空間。





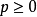

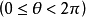
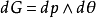

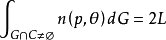





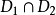
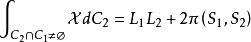
積分幾何學是通過各種積分考察圖形性質的一門學科,本質上屬於整體微分幾何範疇。積分幾何的研究從歐氏平面和三維歐氏空間開始,逐步拓廣到高維歐氏和非歐空間,然後概括...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
它是數學的一個基礎學科,內容主要包括極限、微分學、積分學及其套用。微分學包括...緊接著函式概念的採用,產生了微積分,它是繼歐幾里得幾何之後,全部數學中的一個...
英文Geometry一詞,是從希臘語演變而來的,其原意是土地測量、後被我國明朝的徐光啟翻譯成"幾何學"。依據大量實證研究,創造幾何學的是埃及人,幾何學因...
不可分量幾何學(Ueometria indivisibilibus con一tinuorum nova quadam ratione promota ) 17世紀西方數學著作.直譯為《運用連續體的不可分量以新方式推進的幾何學...
積分幾何(integral geometry)數學中通過各種積分研究圖形性質的一門學科,本質上屬於整體微分幾何範疇。...
高斯積分是在機率論和連續傅立葉變換等的統一化等計算中有廣泛的套用。在誤差函式的定義中它也出現。雖然誤差函式沒有初等函式,但是高斯積分可以通過微積分學的手段...
(x,y)在D上的二重積分≤ MS這就是二重積分的估值定理 如果是一元函式f(x)...《關於曲面的一般研究》,全面系統的闡述了空間曲面的微分幾何學,並提出內蘊曲面...
成為分析的“分水嶺”,人們常把勒貝格以前的分析學稱為經典分析,而把以由勒貝格...因此,在理論和套用上都迫切要求建立一種新的積分,它既能保持R積分的幾何直觀和...
博赫納積分是勒貝格積分在向量值函式情形的直接推廣,是由博赫納(S.Bochner)在1932年建立的,這種積分在向量值測度理論、運算元理論、機率論、隨機過程以及巴拿赫空間幾何...
均質積分(quermass integral)亦稱平均截面測度.凸體論和積分幾何的重要概念.本質上是R"中凸集在((n-r)維平面上投影體積的積分平均值.若K為R"中的凸集,L。一...
無限維分析學的一個新分支。它起源於量子物理學中的連續積分和機率論中的隨機過程的樣本空間的研究。目前,泛函積分方法已深入到分理化量子場論、基本粒子理論、隨機...
定積分的元素法是在套用定積分的理論來分析和解決一些幾何,物理中的問題時,需要將一個量表達成為定積分的分析方法。...
二重積分幾何意義 在空間直角坐標系中,二重積分是各部分區域上柱體體積的代數和,在xoy平面上方的取正,在xoy平面下方的取負。某些特殊的被積函式f(x,y)的所表示...
它和擬微分運算元一起,被稱為“70年代技術”。擬微分運算元的前身是具強奇性的卷積型奇異積分運算元。傅立葉積分運算元產生於用幾何光學方法求經典波動過程的漸近表達式及...
