定積分的元素法是在套用定積分的理論來分析和解決一些幾何，物理中的問題時，需要將一個量表達成為定積分的分析方法。
步驟
一般的，如果某一實際問題中的所求量U符合下列條件：
（1）U是一個變數x的變化區間[a,b]有關的量；
（2）U對於區間[a,b]具有可加性，就是說，如果把區間[a,b]分成許多小區間，則U相應的分成許多部分量，而U等於所有部分量之和；
（3）部分量
近似值可表示為
，那么就可以考慮用定積分來表達這個量U。通常寫出這個量U的積分表達式的步驟是：
1）根據問題的具體情況，選取一個變數例如x為積分變數，並確定他的變化區間[a,b]；
2）構想把區間[a,b]分成n個小區間，選取其中任一個小區間並記作[x,x+dx]，求出相應於這個小區間的部分量△U的近似值。如果△U能近似的表示為[a,b]上的一個連續函式在x處的值f(x)於定積分dx的乘積，就把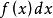
稱為量U的元素且記作dU，即
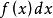
3）以所求量U的元素
為被積表達式，在區間[a,b]上作定積分，得
這就是所求量U的積分表達式。
上面所用的方法就是元素法。
