基本介紹
- 中文名:解析開拓
- 外文名:Analytic continuation
- 實質:定義域擴大的過程
- 關係:ƒ1和ƒ2
- 學科:數理科學
- 定義:解析函式的定義域擴大的過程
簡介
定義
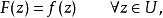

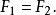
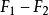
解析介紹
施瓦茲對稱原理
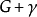
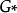
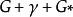
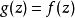
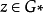
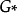
此外,ƒ在γ上可以改為取值平面上某圓周上的值。更一般的情況,如果ƒ的定義域G的邊界有一段解析弧γ,ƒ在

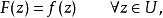

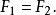
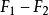
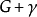
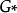
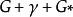
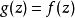
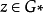

解析延拓,是數學上將解析函式從較小定義域拓展到更大定義域的方法。實質是定義域擴大的過程。透過此方法,一些原先發散的級數在新的定義域可具有迥異而有限的值。...
解析開拓原理是擴大解析函式定義域的原理。解析延拓是數學上將解析函式從較小定義域拓展到更大定義域的方法。...
直接解析開拓(direct analytic continuation)是滿足解析開拓原理的兩解析元素。若給定兩個解析元素{D1,f(z)}及{D2,f(z)},D1和D2互不包含,其公共部分是一...
若每一個解析元素都是前一個解析元素的直接解析開拓,則稱這些解析元素組成解析開拓鏈,並稱{D1,f1(z)}及{Dn,fn(z)}互為解析開拓。...
基於魏爾斯特拉斯的定義,區域上的解析函式可以看作是其內任一小圓鄰域上冪級數的解析開拓 ,關於解析開拓的一般定義是,f(z)與g(z)分別是D與D*上的解析函式,...
完全解析函式(complete analytic function) 亦稱整體解析函式,一類大範圍解析函式中一個解析元素的全部解析開拓所確定的函式稱為由這個解析元素生成的完全解析函式,它的...
解析運算元半群是一類特殊的壓縮半群,這類半群在拋物型方程中有重要套用。...... 解析開拓通常有兩種方法,一種是利用冪級數進行解析開拓,這是外爾斯特拉斯的貢獻。另...
設{D1,f1(z)}及{D2,f2(z)}為兩解析元素,當 x∈D1時,F(z)=f1(z);當 z∈Γ時,F(z)=f1(z)=f2(z);當z∈D2時,F(z)=f2(z),此時稱{D1...
解析函式論(analytic function theory)是複變函數論的主要研究對象,如果說以測度為基礎的實變函式論是研究那些性質不大“好”的函式的話,那么,解析函式論則是研究...
具有支點的完全解析函式稱為多值解析函式。完全解析函式亦稱整體解析函式,一類大範圍解析函式中一個解析元素的全部解析開拓所確定的函式稱為由這個解析元素生成的完全...
解析函式分支(branch of analytic function ) 由完全照一析函式的一個函式元素在區域內的解析開拓所得的函式元素之全體.設f(z)是一個完全解析函式,P(z;a)是f...
黎曼-施瓦茲對稱原理亦稱黎曼-施瓦茲反射原理,是解析開拓的一種方法。...... 黎曼-施瓦茲對稱原理亦稱黎曼-施瓦茲反射原理,是解析開拓的一種方法。中文名 黎曼-施瓦茲...
當D為單連通區域時,如果以D內沿以a為起點的所有曲線都可以解析開拓,則f(z)在D內由P(z;a)確定的分支是單值的,這便是單值性定理。...
方企勤所著圖書。包括習題解析、典型實例精解、結構化學實習三部分...... 1解析開拓概念與冪級數解析開拓 1.1解析開拓概念 1.2冪級數的解析開拓 2對稱原理 3單值...
第六章解析開拓和無窮乘積6.1解析開拓6.2冪級數的解析開拓6.3無窮乘積6.4Γ函式,Beta函式和Riemannzeta函式習題六參考文獻索引 [1] ...
3.6 解析開拓習題三第四章 Riemann映射定理4.1 共形映射4.2 正規族4.3 Riemann映射定理4.4 對稱原理4.5 Riemann曲面舉例4.6 Schwarz-Christoffel公式習題四...
