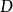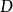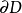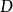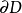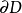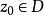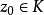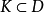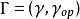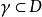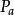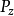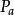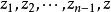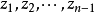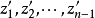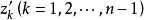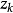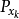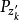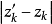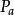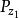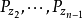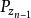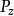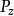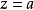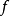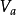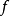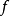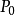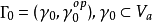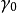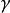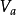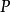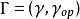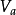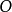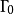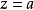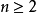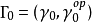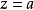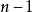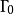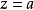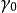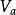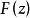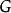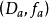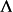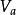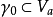完全解析函式

完全解析函式（complete analytic function） 亦稱整體解析函式，一類大範圍解析函式中一個解析元素的全部解析開拓所確定的函式稱為由這個解析元素生成的完全解析函式，它的定義域 G 稱為它的存在域，G 的邊界稱為這個完全解析函式的自然邊界，G的邊界點就是這個完全解析函式的奇點。一個完全解析函式可能是單值的，也可能是多值的。此外，如果兩個完全解析函式至少有一個共同元素，則這兩個函式被認為是相等的。

基本介紹

• 中文名：完全解析函式
• 外文名：complete analytic function
• 別名：整體解析函式
• 類型：單值的、多值的
• 特點：不依賴於初始元素的選擇
• 套用學科：複變函數

定義

若函式在區域 內解析，且區域 的邊界 上每一點都是它的奇點，則它就不能越過區域 的任意一部分邊界解析開拓；若在 上有正則點，則此函式就可以越過邊界 解析開拓出去。對於開拓後得到的函式及區域，還可以再研究它能否進一步解析開拓，這樣就可以不斷地解析開拓，一直到不能開拓為止。為了刻畫這個事實，需要引進完全解析函式的概念。

設所有標準元素集合由任一元素 P 沿所有若爾當曲線作解析開拓而得到，此曲線起點在元素 P 的圓心，且對此曲線可以作解析開拓，則稱這個標準元素集合為完全解析函式。我們指出，完全解析函式的概念不依賴於初始元素 P 的選擇。實際上，設 Q 是由初始元素 P 確定的完全解析函式的任一其他元素，這表示 Q 是由 P 沿著某條曲線開拓得出的。於是 P 可以由 Q 沿曲線開拓得出。如果兩個完全解析函式至少有一個共同元素，則這兩個函式被認為是相等的。

一個完全解析函式 是一個一般解析函式，它包含其任一元素的所有解析開拓， 的定義域 稱為它的存在區域， 的邊界稱為 的自然邊界。

相關定理

定理1

定理內容：屬於完全解析函式的諸元素收斂圓的並集構成一個區域。

證明：設 D 是這個並集，它作為諸開集的並集是一個開集，即如果 ，則 是某一元素的收斂圓，且 。設 a 與 b 是集 D 的任意兩點，則可求出兩個元素，使得a 與 b 是它們的圓心。這兩個元素是沿某一路線 互為解析開拓而得出的，這條路線是連結點 a 與 b 而成的。顯然 ，因此 D 是連通開集，即一個區域，它稱為完全解析函式的自然定義域或它的存在域。

我們指出，完全解析函式不能是區域 D 內廣義的函式，因為它不是單值的。

定理2

定理內容：完全解析函式含有不多於圓心在一定點處的可數多個不同元素。

證明：設完全解析函式由圓心在點 a 處的初始元素 確定，z 是完全解析函式定義域 D 中的任意一點。設 是完全解析函式的一個元素，圓心在點 z 處，它可由元素 用圓心在點 的有限元素鏈得出，其中每後一個元素都是前一元素的直接解析開拓。不是一般性，可以設諸點 有有理坐標。實際上，首先設圓心 是任意的。在點 的任意小的領域內取一個帶有理坐標的點 ，並用元素 代替 ，根據沿路線解析開拓關於路線同倫形變的不變性定理，在 充分小時，按新鏈開拓的結果和按舊鏈開拓的結果相同。具有元素 有理圓心的元素 直接解析開拓集合是可數的，恰好與元素 的可數集一樣。給定 與點 z 就唯一地確定了元素 ，因此不同元素 的個數不超過可數集。

注意：研究完全解析函式的概念，不一定只利用標準元素，可以取任意元素，把完全解析函式看作是解析元素集合 ，其中 a 取遍某一指標集 ，這時元素中的每一個元素可由任意其他元素解析開拓得出。

奇點

奇點的定義

完全解析函式定義域的邊界點稱為它的奇點。

設 是完全解析函式 的一個孤立奇點， 是 定義域 D 內的一個去心鄰域。

引理

如果任一屬於 的標準元素 在沿著某閉路線 作解析開拓時沒有改變，則當若當曲線 與 在 內作解析開拓得出的任一元素 ，在沿任一路線 開拓時沒有改變。

注意：由該引理可推出，在 內沿著與 同倫的路線解析開拓不改變元素，這樣的路線被收縮為任一元素的圓內路線，沿這些路線的解析開拓不改變元素。

單/多值特徵的奇點

設 是完全解析函式 的孤立奇點， 是此點在 定義域內的去心鄰域， 是包圍點 的閉若當曲線，於是，如果：

（1）沿曲線 繞行將得到初始元素，則 稱為單值特徵的奇點；

（2）沿 繞行得到不同初始元素的元素，則 稱為多值特徵的奇點或支點。

n-1階/無窮階支點

設 是完全解析函式 的支點， 是包圍點 的閉若爾當曲線，於是，如果：

（1）存在這樣一個整數 ，使 次同方向繞行 得到初始元素，並且 是具有上述性質的所有整數中的最小值，則 稱為 階支點；

（2）若不存在（1）中所述的整數，即同方向繞行 得出新而又新的元素，則 稱為無窮階階支點或對數支點。

注意：容易檢驗，如果把曲線 換為 內與 同倫的任一若爾當曲線 ，則支點的階數不變。