若f(z)在z0不解析,但在z0的某一去心鄰域0<|z-z0|<δ內解析,則稱z0是f(z)的孤立奇點,根據其洛朗級數的情況,可將其分為可去奇點、(m級)極點和本性奇點。
基本介紹
- 中文名:孤立奇點
- 外文名:isolated singular point
- 學科:數學
- 分類:可去奇點;極點;本性奇點
- 分類判別:極限
- 聯繫:留數
定義



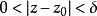





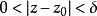


可去奇點


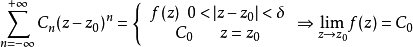



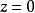
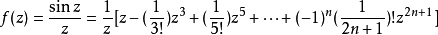
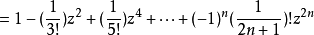
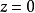
極點



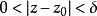



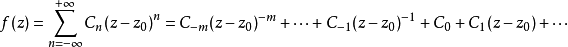
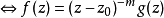
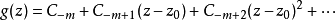


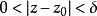
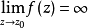


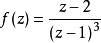
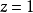
本性奇點



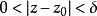



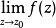
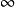


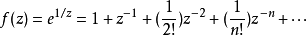


分類判別規則


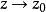


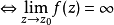

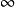
無窮遠處
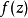
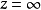
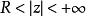

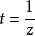
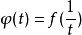

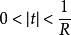
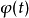
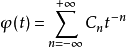
 圖1 f(z)無窮遠處的性態
圖1 f(z)無窮遠處的性態若f(z)在z0不解析,但在z0的某一去心鄰域0<|z-z0|<δ內解析,則稱z0是f(z)的孤立奇點,根據其洛朗級數的情況,可將其分為可去奇點、(m級)極點和本性奇點。



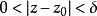





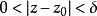




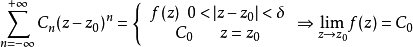



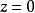
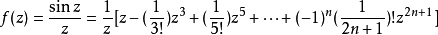
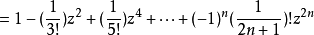
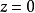



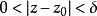



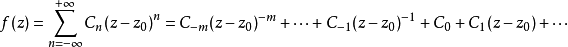
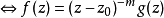
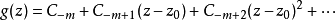


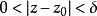
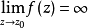


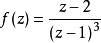
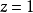



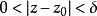



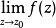
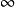


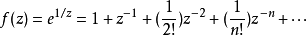




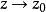


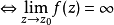

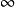
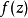
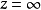
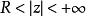

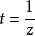
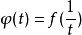

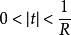
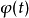
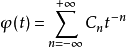
 圖1 f(z)無窮遠處的性態
圖1 f(z)無窮遠處的性態若f(z)在z0不解析,但在z0的某一去心鄰域0<|z-z0|<δ內解析,則稱z0是f(z)的孤立奇點,根據其洛朗級數的情況,可將其分為可去奇點、(m級)極點和本性...
《完全交上的孤立奇點》是2013年高等教育出版社出版的圖書,作者是路易安嘎。...... 《完全交上的孤立奇點》是2013年高等教育出版社出版的圖書,作者是路易安嘎。...
在複分析中,一個函式的本性奇點(Essential Singularity)又稱本質奇點,是奇點中的“嚴謹”的一類。...
在複分析中,一個全純函式的可去奇點(removable singularity),有時稱為裝飾性奇點(cosmetic singularity)是這樣的點,在此處函式表面上沒有定義,但是通過細緻地分析,...
如果以復變數為變數的函式在點a的洛朗展式中的主要部分為無限多項,則稱a為此函式的本質奇點。...
解析函式奇點,數學概念,即函式不解析的點。...... 孤立奇點分為:可去奇點、極點和本性奇點。判定方法是:當z趨於z0時,若f(z)的值有限,則稱改點為可去奇點,...
奇點解消是代數幾何中最重要的技術工具之一。...... 假設V是一個代數簇, P是V上的一個孤立奇點,U是包含P的一個鄰域 ,如果存在一個光滑的代數簇的開集 W,...
奇點指標(index of a singularity)描述孤立奇點拓撲性態的一個量.設X是微分流形M上的連續向量場,pEM是X的孤立奇點.設VCM是含P的拓撲n維球,這裡n=dimM,要求Y...
《複變函數奇點》的作者是謝力之 / 劉中興,電子工業出版社出版...... 《複變函數奇點》的作者是謝力之 / 劉中興...第二章 孤立奇點 第三章 留數定義及計算...
留數是複變函數中的一個重要概念,指解析函式沿著某一圓環域內包圍某一孤立奇點的任一正向簡單閉曲線的積分值除以2πi。留數數值上等於解析函式的洛朗展開式中負...
全書共7章,內容包括:複數與複變函數,解析函式的概念與初等解析函式,複變函數的積分,解析函式的冪級數表示,解析函式的羅朗展式與孤立奇點,留數理論及其套用,共形...
5.2孤立奇點的分類與判定習題5第6章留數定理、輻角原理和魯歇定理6.1留數定理6.2利用留數計算實積分6.3輻角原理6.4魯歇定理及其套用6.5Huiwitz定理、單葉性...
《高等學校教材:複變函數論(第四版)》內容包括:複數與複變函數、解析函式、複變函數的積分、解析函式的冪級數表示法、解析函式的洛朗展式與孤立奇點、留數理論...
全書的主要內容有:複平面上的複變函數、解析函式的微積分、孤立奇點的處理方法、與解析函式有關的若干套用問題、保形映照、積分變換和習題精選與解題指導等七章。...
