在複分析中,一個函式的本性奇點(Essential Singularity)又稱本質奇點,是奇點中的“嚴謹”的一類。
基本介紹
- 中文名:本性奇點
- 外文名:Essential Singularity
- 類屬:數學
- 別名:本質奇點
- 條件:奇點為孤立奇點
- 本質:一個確定點
定義


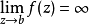





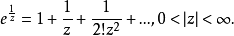



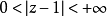

本性奇點的特性
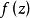
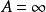





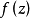
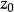



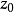




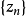
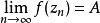






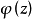
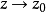




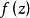









在複分析中,一個函式的本性奇點(Essential Singularity)又稱本質奇點,是奇點中的“嚴謹”的一類。


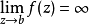





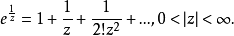



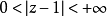

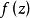
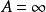





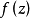
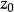



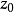




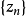
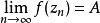






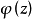
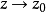




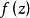









在複分析中,一個函式的本性奇點(Essential Singularity)又稱本質奇點,是奇點中的“嚴謹”的一類。...
函式不解析的點.若函式f(z)在點z=u 的任一鄰域內不能展為泰勒級數,則點z=u稱為 f (z)的一個奇點一個函式的奇點可以是單值性奇點,也可以是多值性奇點...
皮卡小定理可以從皮卡大定理推出,因為整函式要么是多項式,要么在無窮遠處具有本性奇點。 [1] 皮卡定理皮卡定理介紹 編輯 皮卡定理是兩個不同的數學定理的泛稱,...
一個既不是極點又不是分支點的非可去奇點稱為本性奇點。 除了一些孤立奇點外全純的函式,且所有的奇點均為極點,則該函式稱為亞純函式。多...
皮卡大定理說明,如果f(z)在點w具有本性奇點,那么在任何含有w的開集中,對任意非∞的複數值A,有無窮多個z使得f(z)=A,A最多只有一個例外。 以上定理是說,...
留數是複變函數中的一個重要概念,指解析函式沿著某一圓環域內包圍某一孤立奇點的任一正向簡單閉曲線的積分值除以2πi。留數數值上等於解析函式的洛朗展開式中負...
但射影簇都是代數的(周緯良(Chow)定理),用完全可能含許多本性奇點的解析函式,來研究這些代數對象是有點不自然。很清楚,利用有理函式應該就夠了---事實也正如...
(z)在一區域0z|ρ為全純並以z=0為本性奇點,則在此區域內函式?(z)取每一有窮值無窮次,最多除去一個例外值。根據蒙泰爾的正規性定則還可以證明下列朔特基...
碰撞時刻 t 是多體運動方程的奇點。當時間趨於t 時﹐碰撞質點的相互距離趨於零﹐監於萬有引力與距離平方成反比﹐所以加速度趨於無窮大﹐微分方程在該點不再滿足...
當∞點是整函式的本性奇點時,這個整函式的泰勒展式一定有無限多項,這類整函式稱為超越整函式。由代數基本定理知道n次多項式一定有n個零點(也就是根),它總可以...
w是M上的一個點,PC=C∪{∞}表示黎曼球面,f:M\{w}→PC是一個全純函式,在w處具有本性奇點,那么在M的任何含有w的開子集中,函式f都可以取得除了兩個點以...
比如有理函式就是在擴充複平面上的亞純函式,它是兩個多項式的商而Q(z)的零點是R(z)的極點,即R(z)有有限多個極點,∞點是R(z)的極點或可去奇點。複平面...
[2] 他研究了解析函式在本性奇點附近的性態,提出並證明了下列定理:如果a是f (.x)的本性奇點,則對任何複數C,存在收斂於a的點列En(n一1,2,}}})使f (...
比如有理函式就是在擴充複平面上的亞純函式,它是兩個多項式的商而Q(z)的零點是R(z)的極點,即R(z)有有限多個極點,∞點是R(z)的極點或可去奇點。複平面...
給外爾斯特拉斯定理——解析函式可任意接近其本性奇點鄰域中的每一個值——提供了第一個完整的證明。研究了其冪級數在收斂圓周上的點發散的解析函式。論證了它們在...
如前一節所述,調和函式的孤立奇點可分類為可去除奇點、極點與本性奇點。 [3] 位勢論不等式 編輯 研究調和函式的一種卓有成效的辦法是研究它們滿足的不等式,...
他把整函式定義為在全平面上都能表示為收斂的冪級數的和的函式;還斷定,若整函式不是多項式,則在無窮遠點有一個本性奇點。魏爾斯特拉斯關於解析函式的研究成果,...
微分方程的解出現的奇點較解析函式論中的情況要複雜得多。首先當自變數圍繞某些點轉一圈以後,函式從一個值變為另一個值,稱這些點為分支點。代數函式可能具有的...
《複變函數論》共分為九章,作者從複變函數論的基礎講起,由淺入深,並在後兩章中分別講述了奇點、複變函數論在代數和分析上的套用以及保角映俅、複變函數論在...
§1孤立奇點 1.可去奇點 2.極點 3.本性奇點 4.函式的零點與極點的關係 5.函式在無窮遠點的性態 §2留數 1.留數的定義及留數定理 2.留數的計算規則 3...
三、本性奇點第二節 留數定理及留數的求法一、留數的概念二、留數的求法三、雜題第三節 用留數定理計算實積分第四章 總結一、內容小結...
