基本介紹
- 中文名:常微分方程解析理論
- 外文名:analytical theory of ordinary differential equation
- 套用:研究微分方程的性狀
- 方程定義:解析函式
- 性質的理論:並直接從微分方程本身研究解
簡介
解的存在性和惟一性定理
奇點
線性常微分方程
勒讓德方程
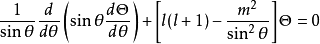
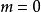
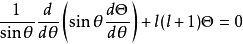
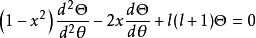

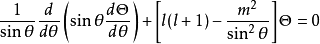
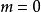
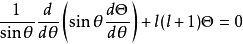
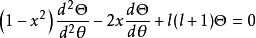
常微分方程解析理論是在複數域上研究微分方程解的性質的數學分支,19世紀中葉,柯西(Cauchy,A,-L)證明了在相當廣泛的條件下微分方程的解是復變數的解析函式,由此...
初等常微分方程,能用微積分的方法求出其通解或通積分的常微分方程。...... 復變數的黎卡提方程在常微分方程解析理論中也有它的重要性,因為它是只可能有動極點...
超球微分方程(hyperspherical equation)是數學物理中常見的常微分方程之一。連帶勒讓德方程經因變數變換後,可以得到超球微分方程;勒讓德方程和格根鮑爾方程都是它...
在從事熱流動的研究中,寫出了《熱的解析理論》,在文章中他提出了三維空間的熱方程,也就是一種偏微分方程。他的研究對偏微分方程的發展的影響是很大的。...
亞純函式奈望林納理論還被推廣於代數體函式、亞純曲線和多復變亞純映射等方面,並且成為研究復域常微分方程解析理論的有力工具。亞純函式值分布理論亞純函式 編輯...
1948年,他在武漢大學《理科季刊》上發表了一批關於概周期函式的準解析性的判定準則,研究了該理論在常微分方程組準解析解方面的套用。 他是準解析函式與函式逼近...
常微分方程 初等常微分方程 線性常微分方程 常微分方程初值問題 常微分方程邊值問題 常微分方程解析理論 常微分方程定性理論 常微分方程運動穩定性理論 泛...
常微分方程 初等常微分方程 常微分方程解析理論 常微分方程定性理論 常微分方程運動穩定性理論 常微分方程攝動方法 偏微分方程 數學物理方程 哈密頓—雅...
a:定性理論 b:穩定性理論 c:解析理論 d:常微分方程其他學科 12:偏微分方程 a:橢圓型偏微分方程 b:雙曲型偏微分方程 c:拋物型偏微分方程 d:非線性偏微分方...
長期從事數學領域的研究和教學工作,在常微分方程穩定性理論方面的研究有較高的...解放後,許淞慶一直在中山大學數學講壇上執教,任教過多門基礎課(如微積分,解析...
《自守函式論》是十九世紀群論在函式論中的套用,其理論是幾何學、代數學、複分析、微分方程解析理論交叉的產物,體現了數學的統一性。...
前4個領域是關於複分析方面的,他第一個有意識的將實域過渡到復域,開創了複變函數域,代數函式論,常微分方程解析理論及解析數論諸方向;後4個領域主要涉及實分析,...
第二基本定理是亞純函式奈望林納理論中重要定理。奈望林納在亞純函式的研究中...亞純曲線和多復變亞純映射等方面,並且成為研究復域常微分方程解析理論的有力...
