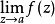如果以復變數為變數的函式在點a的洛朗展式中的主要部分為無限多項,則稱a為此函式的本質奇點。
基本介紹
- 中文名:本質奇點
- 外文名:Essential singularity
- 拼音:běn zhì qí diǎn
- 所屬:數學
- 分類:函式
本質奇點的定義,本質奇點附近的行為,形式描述,替代描述,
本質奇點的定義
粗略來說,對複平面 C 上的給定的開子集 U,以及 U 中的一點 a,亞純函式 f : U\{a} → C 在 a 處有本質奇點若且唯若它不是極點也不是可去奇點。
在複雜的分析中,函式的一個基本奇點是一個“嚴重的”奇點,在這個奇點附近,函式表現出奇怪的行為。
類別本質的奇點是一個“殘留的”或默認的奇點組,尤其是無法管理的:根據定義,它們都不適合於可能以某種方式處理的另外兩類奇點 -可移動的奇點和極點。
本質奇點附近的行為
在複分析中,一個函式的本質奇點(Essential Singularity)是奇點中的“嚴謹”的一類。函式在本質奇點附近會有“極端”的行為。
形式描述
例如,函式f(z)=e在z= 0處有一個基本的奇點。
替代描述
讓一個是複數,假設˚F(ż)在沒有定義一個,但是是解析在一些區域ü複平面的,並且每一個開放附近的一個具有非空交集ù。
如果兩個


如果
同樣,如果

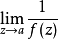
如果兩者都不


表征一個基本奇點的另一種方法是,勞倫系列的˚F在點一個具有無限多的負程度術語(即,主要部分的勞倫系列是一個無限總和)。一個相關的定義是,如果有一個點 對此沒有任何派生的
對此沒有任何派生的 收斂到極限
收斂到極限  傾向於
傾向於  , 然後
, 然後  是一個重要的奇點
是一個重要的奇點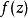 。
。





全純函式在其基本奇點附近的行為由Casorati-Weierstrass定理和相當強大的Picard定理描述。後者說,在每個基本奇點a的鄰域中,函式f對任何複雜的價值(無論是否可能是一個)都有無窮無盡的多次。(這個例外是必要的,因為函式exp(1 /z)永遠不會取0的值)。