有界平均振動解析函式

有界平均振動解析函式是哈代空間H¹的對偶空間中的函式。單位圓盤的解析函式f(z)若能表為一個有界平均振動函式的泊松積分，則稱它屬於有界平均振動解析函式。

基本介紹

• 中文名：有界平均振動解析函式
• 外文名：analytic function ofbounded mean oscillation
• 適用範圍：數理科學

簡介

有界平均振動解析函式是哈代空間H¹的對偶空間中的函式。

有界平均振動函式

有界平均振動函式有種種等價描述，其原始定義如下：

對於單位圓周T上的可積函式u，若I是T的子弧，令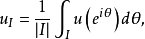

這裡|I|是I的長度。若

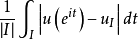對T上的一切子弧I有界，則稱u屬於BMO（有界平均振動函式的簡稱）。

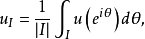
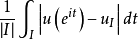
有界平均振動解析函式

單位圓盤的解析函式f(z)若能表為一個BMO函式的泊松積分，則稱它屬於BMOA（有界平均振動解析函式的簡稱）。

哈代空間

哈代空間是單位圓內一類重要的解析函式空間。是由數學家哈代(Hardy，G.H.)在1915年首先提出的。在複分析中，哈代空間（或哈代類）H是單位圓盤或上半平面上的某類全純函式。高德菲·哈羅德·哈代首先在1915年考慮這類問題。在實分析中，實哈代空間是復哈代空間的成員在實數軸上的邊界值。

在較高維的情況，我們可考慮管狀域（複數情形）的函式，從而得到相應的定義。哈代空間在數學分析、控制論及散射理論中有所套用。