基本介紹
- 中文名:同倫
- 外文名:Homotopy
- 相關術語:拓撲空間
- 套用學科:數學
- 所屬領域:數學
- 定義:描述了兩個對象間的“連續變化”
描述
產生
函式的同倫


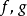
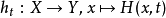
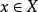

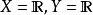
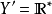
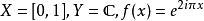
相對同倫
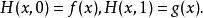
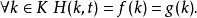

空間同倫等價
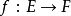
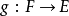

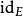


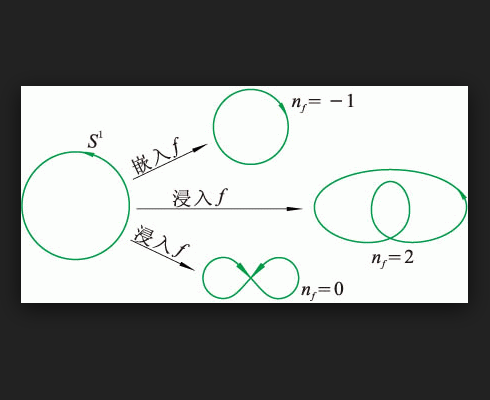


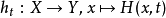
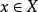

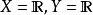
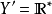
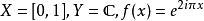
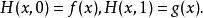
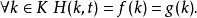

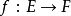
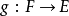

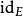


在數學中,同倫(Homotopy)的概念在拓撲上描述了兩個對象間的“連續變化”。兩個拓撲空間如果可以通過一系列連續的形變從一個變到另一個,那么就稱這兩個拓撲空間...
同倫論是拓撲學的重要概念。應該指出,映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合上的一個 等價關係,它將這些映射分成一些等價類,稱每個等價類為一...
同倫映射(homotopic maps)是拓撲學中的重要概念。應該指出,映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合C(X,Y)上的一個等價關係,它將這些映射分成...
同倫群(homotopy groups)是基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。相對同倫(relative homotopy)是同倫群的推廣。...
同倫運算元(homotopy operator)是具有同倫性質的線性變換。兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。倫型相同...
在數學的拓撲學領域中,同倫範疇是處理同倫問題時格外便利的範疇論語言。...... 在數學的拓撲學領域中,同倫範疇是處理同倫問題時格外便利的範疇論語言。...
方法特點 同倫拓展法h}rnotapic cantinu<
同倫等價空間(homotopy equivalent spaces)是利用映射的同倫關係給出的拓撲空間的另一種分類,在拓撲學中具有重要地位。若兩個拓撲空間X和Y之間存在一對連續映射f:...
同倫切除定理是同倫論的一個重要定理。同倫群與同調群有很多相似的性質,如同倫型不變性、正合序列等,但是兩者也有一些本質區別。...
同倫型不變性質(homotopy type invariance)是拓撲學的一種重要不變性質。具有相同同倫型的拓撲空間所共有的性質稱為同倫型不變性質。拓撲學是數學的一個分支。...
同倫類型論(homotopy type theory,縮寫HoTT)是一套旨在於同倫論的大框架下構建內涵類型論語義的理論,尤指Quillen模型範疇和弱分解系統。...
同倫資產管理有限公司於2010年08月12日在南京市江寧區市場監督管理局登記成立。法定代表人潘欣,公司經營範圍包括資產管理;投資管理;契約能源管理;項目投資等。...
正合同倫序列(exact homotopy sequence)是同倫的重要性質之一。是聯繫(絕對)同倫與相對同倫的一種關係。倫型相同的拓撲空間所共有的性質稱為同倫不變數。由於...
向同倫 。中共重慶市涪陵區委黨史研究室副研究員。畢業於龍潭高中。1950年4月參加革命,歷任宣傳幹事、團區委書記、副區長、縣委秘書,涪陵地委黨史工委專職副主任,...
《同倫方法縱橫談》是2011年5月1日大連理工大學出版社出版的圖書,作者是王則柯。...... 本書主要講述了同倫方法的基本概念、運用知識以及相關的其他數學概念。本書...
《同調與同倫原理》是作者在代數拓撲選修課講義的基礎上,經仔細整理、增刪和潤色而成的。全書共分八章。第0章是對一般拓撲學基本理論的簡要回顧,第1、2兩章...
霍普夫同倫分類定理(Hopf homotopy classification theorem)是布勞威爾度的同倫不變性定理的一個逆定理。...
翁同倫,翁檉次子、翁同文之二弟。1917年生,浙江泰順縣翁山鄉外洋村人。翁同倫,翁檉次子、翁同文之二弟。1917年生,浙江泰順縣翁山鄉外洋村人。10歲隨父遷居...
白同倫,現任十三屆人大一次會議上當選為包頭市人大常委會副主任。白同倫[1] ,男,回族,1951年10月出生,山東陵縣人,大普文化,1973年9月入黨,1969年4月參加工作。...
弱同倫等價(weakhomotopyequivalence)同倫等價的推廣.設f:X->Y是拓撲空間之間的連續映射,n>0是整數,若對於一切二。EX,當:Gn時,f.:n,(X,xo)-}n,.(Y,...
《同倫分析方法與非線性微分方程(英文版)》介紹同倫分析方法的基本思想、理論上的發展與完善以及新的套用。...
在數學中,有理同倫論是對拓撲空間的有理同倫型的研究,是有理同倫型忽略同倫群的撓。有理同倫論由Dennis Sullivan (1977) 與Daniel Quillen (1969) 首創。...
計算機最佳化同倫算法編輯 鎖定 本書可供高等院校的數學、計算機和管理、工程力學等專業研究生或高年級學生以及從事最佳化研究和套用的科技人員使用。[1] ...
《超越攝動:同倫分析方法導論》系統地介紹了廖世俊教授原創性地提出的一種求解非線性問題的一般方法,即"同倫分析方法",描述了整個理論體系的完整框架,詳細地介紹了...
