同倫運算元(homotopy operator)是具有同倫性質的線性變換。
兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。
倫型相同的拓撲空間所共有的性質稱為同倫不變數。由於同胚的空間必同倫,故同倫不變數一定是拓撲不變數。代數拓撲學主要研究空間的同倫。
基本介紹
- 中文名:同倫運算元
- 外文名:homotopy operator
- 領域:數學
- 性質:線性變換
- 特點:同倫
- 對象:微分流形
概念,同倫,線性變換,微分流形,
概念
同倫運算元(homotopy operator)是具有同倫性質的線性變換。設f1,f2是兩個微分流形M,N之間的C∞映射,則有誘導映射:
δfi:Ek(N)→Ek(M) (i=1,2),
k為非負整數,對於這些誘導映射,若存在一組線性變換hk:Ek(N)→Ek-1(M),使得

則稱這組線性變換{hk}為f1與f2的同倫運算元。可以看出龐加萊引理中的{hk}也是同倫運算元。
同倫
H(x,0)=f(x)
H(x,1)=gx∈X
則稱f與g同倫,記為f≃g:X→Y或f≃g,映射H稱為f與g之間的一個同倫。f與g的同倫H也可理解為單參數映射族{ht}t∈I,ht連續地依賴於t且h0=f,h1=g,即當參數t從0變到1時,映射f連續地形變為g。與常值映射同倫的映射稱為零倫的。若以C[X,Y]表示X到Y的一切連續映射之集,則同倫關係≃是C[X,Y]上等價關係,每個等價類稱為一個同倫類,同倫類的全體所成集記為[X,Y]。設Y是R的子空間,f,g:X→Y是連續映射,若對每個x∈X,點f(x)與g(x)可由Y中線段連結,則f≃g:X→Y,若Y是R中凸集,任何映射f:X→Y都零倫,即[X,Y]僅含一個元素。設X,Y與Z均為拓撲空間,若f≃f:X→Y,g≃g: Y→Z,則gf≃gf: X→Z。
設X,Y為拓撲空間,若存在連續映射f:X→Y和g:Y→X,使得gf≃Idx且f·g≃idr。這Id、id均表示恆同映射,則稱f為同倫等價,g為f的同倫逆,而將X與Y稱為具有相同的倫型,或簡稱同倫的,記作X≃Y。與單點空間同倫的空間稱為可縮的,或者存在x0∈X,使得常值映射C:X→X。x1→x0與映射idx同倫,空間X可縮。R和R中凸集均為可縮空間。同倫關係是拓撲空間之間的等價關係。X可縮等價於下列幾條中任意一條:(1)idx≃0,即恆同映射idx零倫。(2) 對任意空間Y,映射f:X→Y,有f≃0。(3)對任意空間Z和連續映射g:Z→X,g≃0。
設A是空間X的子空間,i:A→X表包含映射,若存在連續映射r:X→A,使得r|A=idA(或r·i=idA),則r稱為X到A的保核收縮,A稱為X的收縮核。若有保核收縮r:X→A滿足i·ridx:X→X,則H稱為X到A的形變收縮,A稱為X的形變收縮核,若同倫H還滿足對任意x∈A和t∈I有H(x,t)=x,則H稱為X到A的一個強形變收縮,A稱為X的強形變收縮核。強形變收縮是形變收縮,且若A是X的形變收縮核,則內射i:A→X是同倫等價。
兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。
倫型相同的拓撲空間所共有的性質稱為同倫不變數。由於同胚的空間必同倫,故同倫不變數一定是拓撲不變數。代數拓撲學主要研究空間的同倫。
設A為空間X的子空間,序偶 (X,A) 稱為空間偶,連續映射f: X→Y,把A映到Y的子空間B內,則記f:(X,A)→(Y,B)。若有連續映射f:(X,A)→(Y,B),g:(Y,B)→(X,A)使得g·f=idx,f·g=idY,則f為空間偶的同胚。同樣有偶的同倫的概念。若有偶的同倫:f≃g:(X,A)→(Y,B)滿足:對任意t∈I,x∈A有H(x,t)=f(x)=g(x),稱f和g相對於A同倫,記作:
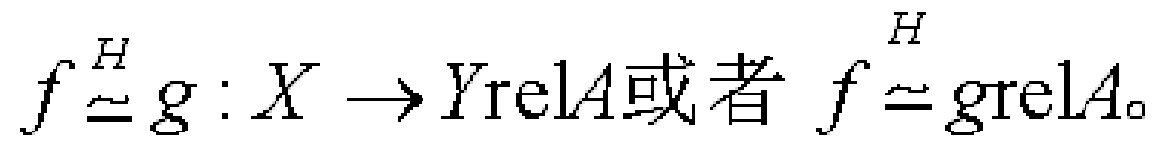
當A為空集∅時,相對同倫就是一般同倫。設A⊂X,則A是X的強形變收縮核的充要條件是:存在收縮映射(保核收縮)r:X→A使得ir≃idx:X→XrelA,其中i:A→X為內射。
線性變換
未知數的線性變換,是一組(m個)未知數x1,x2,…,xm到另一組(n個)未知數y1,y2,…,yn的一個變換,使得新未知數用原未知數線性地表出:
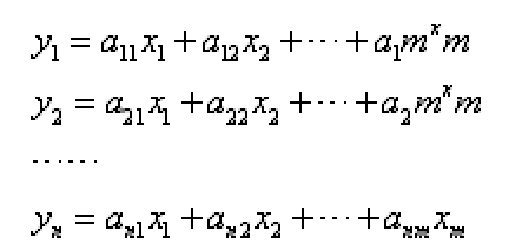
其中係數aij(i=1,2,…n,j=1,2,…,m)為常數。例如,歐氏空間中的旋轉,是一種線性變換。
更一般地,設L是線性空間的一個把向量X1、X2分別變換為向量Y1,Y2的變換,若在變換L下,線性組合a1X1+a2X2變換為a1Y1+a2Y2,則稱變換L為線性變換。
微分流形
設M是仿緊豪斯道夫 (Hau-sdorff)空間,且是拓撲流形,稱A= {(Uα,Фα)|α∈P}是它的地圖,如果{Uα|α∈P}是M的開覆蓋,Фα是從Uα到n維歐氏空間R的某開集上的同胚。(Uα,Φα)稱為坐標卡。如果兩個坐標卡 (Uα,Фα),(Uβ,Φβ) 滿足Uα∩Uβ≠Φ,則稱Φβ·Ф-1α:Φα(Uα∩Uβ) →Φβ(Uα∩Uβ) 和Φα·Φ-1β: Φβ(Uα∩Uβ) →Фα(Uα∩Uβ) 為Uα∩Uβ上的坐標變換。如果A的所有坐標變換都是Cr可微的,則稱A為一個Cr地圖,其中1≤r≤∞。r也可等於ω,此時A稱為解析地圖。拓撲流形M的坐標卡 (U,Φ) 稱為與A是Cr相容的,如果任意(Uα,Φα) ∈A,坐標變換Φ·Φα-1Φα·Φ-1均C可微。拓撲流形M的Cr地圖A稱為最大的,如果它包含M的所有與之Cr相容的坐標卡。M上的最大Cr地圖A稱為M的Cr微分結構。(M,A)稱為Cr微分流形,或簡稱為Cr流形。當r=∞時,C∞微分結構也稱為光滑結構,C∞流形也稱為光滑流形。r=ω時,Cw結構也稱為解析結構,Cw流形稱為解析流形。Cr流形(M,A)有時也簡記為M。
從直觀上看,拓撲流形是局部歐氏空間,局部之間用同胚映射(坐標變換)貼上在一起。n維Cr流形,不僅局部同胚於n維歐氏空間,而且局部之間是用Cr光滑、且其逆也Cr光滑的坐標變換貼上在一起。
兩個Cr流形M和N,f:M→N是連續映射,且任一點P∈M,有包含P點的M中的坐標卡(U,Φ)以及包含f(P)的N中的坐標卡(V,φ),使得f(U)⊂V,同時,映射φ°f°Φ-1:Φ(U)→φ(V)是Cr光滑的(1≤r≤∞或r=ω),則稱f是Cr映射。C∞映射也稱為光滑映射,Cw映射也稱為解析映射。其中φ。f。φ-1稱為f的局部表示。
Cr流形M和N之間的同胚f:M→N,如果f和f-1均是Cr映射,則稱f是Cr微分同胚。
(M,A)是Cr微分流形,A是Cr結構,若1≤r≤s≤∞,則A中包含M的Cs結構A′。且此Cs微分結構A′在相差一個Cs微分同胚的意義下是唯一的,此時我們稱A與A′相容。此結果歸功於惠特尼。同樣,一個C結構也允許相容的實解析結構。這就是說當1≤r<s≤∞時Cr流形與Cs流形無本質區別,特別地Cr流形與C∞流形無本質區別。但如果我們把不存在微分結構的拓撲流形稱為C流形,則C0流形與C1流形有本質區別。存在不允許任何微分結構的拓撲流形,這樣的流形維數最小是四維,已經知道的例子是八維的。
一個拓撲流形M如果存在兩個C∞微分結構A與A′,使微分流形(M,A)與(M,A′)不是C∞微分同胚的,則稱A與A′相異。米爾諾(Milnor)證明七維球S7存在多個相異的C∞微分結構。這種與普通球S同胚,但不是C∞微分同胚的C∞微分流形稱之為怪球。在討論這類問題過程中的一個重要有趣的問題是:“一個光滑流形M,使得M-{P}可縮,其中P是M中任一點,能否引出M同胚於一個球?”對於M的維數n,當n=0,1,2時,M微分同胚於n維球S;當n=3時,歸結為龐加萊猜想;n=4時也未解決;n≥5時,問題結論成立。
微分流形與組合流形的關係,即C剖分與光滑化問題。給n維Cr流形(1≤r≤∞)的一個單純剖分(k,f) (f:|k|→M是同胚)滿足:(1)對於|k|的每個閉n單形σ,f|σ是Cr映射。(2)f|σ的雅可比矩陣的秩在每點均是n,則稱(k,f)是M的Cr剖分,也稱M的Cr結構與剖分(k,f)是Cr相容的。有下面結果:(1)每個Cr流形均具有Cr剖分,且邊緣的Cr剖分可擴張為整個Cr流形的Cr剖分。(2)對於Cr流形M的Cr剖分(k,f),已剖分的空間(k,f,M)是組合流形。(3)對於同一Cr流形M的兩個不同的Cr剖分(k1,f1)和(k2,f2),(k1,f1,M)和(k2,f2,M)組合等價。
反之,如果對於組合流形M,存在M上的微分結構,使剖分(k,i) (其中i:|k|→M是恆等映射)是Cr相容的,則稱之為M的光滑化。現已證明,對於n≤7時,任意n維組合流形可光滑化。
