定義
連續映射(continuous mapping)
拓撲空間之間的一類重要
映射。設(X,T)與(Y,Τ)是兩個拓撲空間,f:X→Y是映射,x∈X。若f(x)的每一鄰域關於f的原像是x的鄰域,則稱f在點x處是連續的。若f在X的任意點是連續的,則稱f是(X,T)到(Y,U)的連續映射。f為連續映射的等價條件有很多,例如:
3.對於任意x∈X和f(x)的任意鄰域U,存在x的
鄰域V使得f(V)⊂U。
4.對於X的每一子集A,有f(cl(A))⊂cl(f(A))。
5.對於Y的每一子集B,有cl(f^(-1)(B))⊂f^(-1)(cl(B)).
6.對於任意s∈X和X中每一收斂於s的網{Sn,n∈D,≤} ,Y中的網{f(Sn),n∈D,≤}
收斂於 f(s). 抽象空間的連續映射是
弗雷歇(Fréchet, M. -R.)於1910年開始考慮的.
 圖一 連續映射的直觀表達示意圖
圖一 連續映射的直觀表達示意圖在
點集拓撲學中.映射的
連續性可用ε一δ語言描述,也可用於開集對應來描述。前者適用於度量空間.後者適用於抽象拓撲空間,為了點集拓撲學與數學分析順利連線,先介紹連續性的ε一δ語言描述,後介紹連續性的開集對應描述。
連續映射的ε一δ語言描述
連續映射用ε一δ語言描述必須分成在一點連續與在
定義域上連續兩個階段來定義,且適用於兩個度量空間之間的映射:
定義1 設X和Y是兩個度量空間,映射f:X→Y;x0∈X,y0=f(x0).若對任一以y0為中心、ε>0為半徑的開球
(ε),存在以x0為中心、δ>0為半徑的開球
(δ),使f(
(δ)⊂
(ε)。則稱映射f:X→Y在x0處連續.
定義2 設X和Y是兩個度量空間,映射f:X→Y。若映射f在每一點x∈X連續.則稱f:X→Y是連續映射。
註記1:不難看出,兩個度量空問之間映射的連續性用ε一δ語言描述,是用開球對應代替不等式對應。ε一δ的不等式對應只適用於1維度量.ε一δ的開球對應則把連續性的描述擴展到n維
度量。當n>3,開球對應中的開球是n維超開球體。
連續映射的開集對應描述
連續映射用開集對應描述無須分成在一點連續與在定義域上連續兩個階段來定義,且適用於兩個拓撲空間之間的映射。
定義3 設T和J是兩個拓撲空間,映射f:T→J。若每個J中的開集U,其逆象
在T中也是開集,則稱f:T→J連續映射.
註記2:用開集對應描述映射連續性的時候,可以撇開度量性。無須分成在一點連續與在定義域上連續兩個階段,這是ε一δ語言與開集語言的最大區別。
相關定理
定理1 設f:X→Y,g:Y→Z均為連續映射,則
複合映射g。f:X→Z也是連續映射。
從幾何意義看:連續映射把集合X中彼此“靠近”的點,映射後的像在Y中仍彼此“靠近”,也就是經過連續映射,不會破壞集合X的完整性,使圖形不產生破裂。如圖二所示,通過連續映射f將圓周X映射成任意形狀的閉曲線Y,圓周上任意一點x,在閉曲線上的像為y,圓周上x“附近”的點,映射後的像在閉曲線上仍是像點y的“附近”點,保持圖形的完整性。
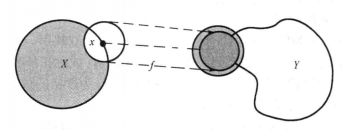 圖二 從圓周到閉曲線的連續映射示意圖
圖二 從圓周到閉曲線的連續映射示意圖如果圖形在映射後產生破裂,如圖三所示,通過映射f將圓周X映射成任意形狀的開曲線Y,圓周上的點x,在開曲線上的像為斷開點y,則圓周上x“附近”的點,映射後的像在開曲線上一部分與像點y“附近”,另一部分與像點y不“附近”,這說明映射f在點x上不連續。
 圖三從圓周到開曲線的不連續映射示意圖
圖三從圓周到開曲線的不連續映射示意圖連續映射保持了圖形的完整性,圖形在變換過程中不會破裂,但可能會出現“粘連”現象。如圖四所示,一個圓周經過連續的變形(即連續映射),最後形成雙扭曲線形狀,那么這個變換過程是連續的,但它將圓周上的不同點a及b映射為同一點,即圖形發生“粘連”現象。這說明連續映射並不能保證圖形不會出現重疊,連續映射還不是我們要找的彈性變換。
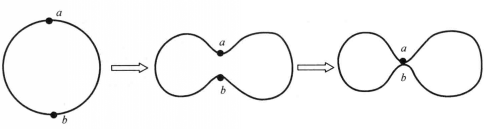 圖四 圓周的連續映射示意圖
圖四 圓周的連續映射示意圖定理2 映射T:(E1,ρ1)→(E2,ρ2)在點Xo∈E1連續若且唯若對任意的ε>0,∃δ>0使得
定理4 映射T:(E1,ρ1)→(E2,ρ2)連續↔任意?>
開集在T下的逆像是開集↔任意
閉集在T下的逆像是閉集.
 圖一 連續映射的直觀表達示意圖
圖一 連續映射的直觀表達示意圖




 圖二 從圓周到閉曲線的連續映射示意圖
圖二 從圓周到閉曲線的連續映射示意圖 圖三從圓周到開曲線的不連續映射示意圖
圖三從圓周到開曲線的不連續映射示意圖 圖四 圓周的連續映射示意圖
圖四 圓周的連續映射示意圖

