令函式是在開區間上可微的,若函式的導函式是開區間上的連續函式,則稱函式在開區間上連續可微,記作。
基本介紹
- 中文名:連續可微
- 外文名:Continuously differentiable
- 套用範圍:數學
- 屬性:函式
定義
一階連續可微



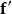














高階連續可微







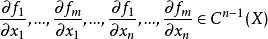

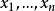


相關定理












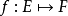






令函式是在開區間上可微的,若函式的導函式是開區間上的連續函式,則稱函式在開區間上連續可微,記作。



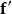





















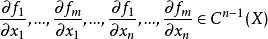

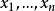














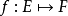






令函式是在開區間上可微的,若函式的導函式是開區間上的連續函式,則稱函式在開區間上連續可微,記作。...
函式的連續性、可導性、可微性是高等數學中的重點和難點內容。一元函式可微與存在導數是等價的。而對於多元函式,偏導數即使都存在,該函式也不一定可微。...
在微積分學中,可微函式是指那些在定義域中所有點都存在導數的函式。可微函式的圖像在定義域內的每一點上必存在非垂直切線。因此,可微函式的圖像是相對光滑的,...
設函式y= f(x),若自變數在點x的改變數Δx與函式相應的改變數Δy有關係Δy=A×Δx+ο(Δx),其中A與Δx無關,則稱函式f(x)在點x可微,並稱AΔx為...
如果一個函式在定義域中的某個點 可微,則它一定在點 連續。反過來不成立;連續的函式不一定可微。例如,絕對值函式在點 連續,但不可微。 [2] ...
連續性方程是質量守恆定律(見質量)在流體力學中的具體表述形式。它的前提是對流體採用連續介質模型,速度和密度都是空間坐標及時間的連續、可微函式。在物理學裡,...
如果運算元半群{Tt|t≥0}滿足條件:當t>0時,對每個x∈X,向量值函式t→Ttx是強可微的,則稱{Tt|t≥0}為可微運算元半群。...
符合利普希茨條件的函式一致連續,也連續。bi-Lipschitz函式是單射的。Rademacher定理:若 且A為開集, 符利普希茨條件,則f幾乎處處可微。 [4] ...
可微映射度(degree of differential map)是重要的同倫不變數。同倫論是拓撲學的重要概念。應該指出,映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合上的...
設Ω為X中的有界集,則f:Ω→Y為全連續映射的充分必要條件是:f能用Ω上的有限維值連續映射一致逼近。可微的全連續映射在每點的導運算元是全連續線性運算元。設D...
可微函式芽環(ring of germs of differentiablefunctions)是一種特殊的環。指可微函式芽的全體在以自然方式定義的加法、乘法下構成的環。考慮n維歐氏空間R上的無窮...
布朗運動是連續鞅,因此也是半鞅。 適應並連續可微過程是有界變差過程,因此也是半鞅。 萊維過程並不一定都是鞅,但一定都是半鞅。半鞅...
1 連續性 2 一致連續性 3 可微性 ▪ 定義 ▪ 可微性的幾何意義 二元函式連續性 編輯 f為定義在點集D上的二元函式.P0為D中的一點.對於任意給定...
