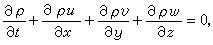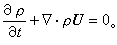連續性方程

連續性方程是質量守恆定律（見質量）在流體力學中的具體表述形式。它的前提是對流體採用連續介質模型，速度和密度都是空間坐標及時間的連續、可微函式。

在物理學裡，連續性方程（continuity equation）乃是描述守恆量傳輸行為的偏微分方程。由於在各自適當條件下，質量、能量、動量、電荷等等，都是守恆量，很多種傳輸行為都可以用連續性方程來描述。

連續性方程乃是定域性的守恆定律方程。與全域性的守恆定律相比，這種守恆定律比較強版。在本條目內的所有關於連續性方程的範例都表達同樣的點子──在任意區域內某種守恆量總量的改變，等於從邊界進入或離去的數量；守恆量不能夠增加或減少，只能夠從某一個位置遷移到另外一個位置。

每一種連續性方程都可以以積分形式表達（使用通量積分），描述任意有限區域內的守恆量；也可以以微分形式表達（使用散度算符），描述任意位置的守恆量。套用散度定理，可以從微分形式推導出積分形式，反之亦然。

基本介紹

• 中文名：連續性方程
• 領域：流體力學
• 前提：對流體採用連續介質模型
• 相關：質量守恆定律

密度不變的流體通過橫截面積A並隨空間坐標s變化的〔即A=A(s)〕一維定常流〔即流速U(s)對於確定的s值不隨時間t改變的情形〕的連續方程最簡單：

AU=常數，

式中U為流速。例如“過堂風”的流速大是因為夾道的橫截面積小。

密度ρ發生顯著變化的一維定常流的連續方程是：

AρU=常數，

對於密度 ρ發生顯著變化的一維不定常流，考慮兩個相隔不遠的橫截面，則流進第一個橫截面的流體比流出第二個橫截面的流體多出的質量就積累在這兩個橫截面之間，因而引起兩個橫截面之間流體密度ρ 隨時間的增長。質量守恆要求：

對於三維不定常流，用 x、y、z表示空間直角坐標，用u、v、w作為質點的速度U的分量，則

或用矢量分析的符號縮寫成：

通過激波或兩種不同密度的流體的交界面，由於ρ和U都不連續,上述方程不再適用，質量守恆定律具有另外的形式。

A1*V1=A2*V2基本公式