霍普夫同倫分類定理

霍普夫同倫分類定理（Hopf homotopy classification theorem）是布勞威爾度的同倫不變性定理的一個逆定理。

基本介紹

• 中文名：霍普夫同倫分類定理
• 外文名：Hopf homotopy classification theorem
• 適用範圍：數理科學

簡介

霍普夫同倫分類定理是布勞威爾度的同倫不變性定理的一個逆定理。

霍普夫同倫分類定理是由霍普夫(Hopf,H.)於1927年得到。

內容

設Ω是Rⁿ中的單位開球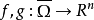， 連續，。若deg(f,Ω,0)=deg(g,Ω,0)，則f與g非退化同倫，即存在連續映射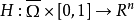，使得H₀=f，H₁=g，且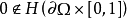。設S為Rⁿ中單位球面，f,g:S→S是兩個連續映射，霍普夫定理可表述為：

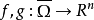
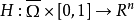
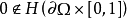
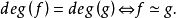
布勞威爾度

布勞威爾度亦稱映射度或拓撲度，是對一類連續映射的一種刻畫。

布勞威爾度套用廣泛，如研究球面上向量場以及博蘇克-烏拉姆定理等。關於布勞威爾度還可推廣到能定向閉假流形以及其他領域中去。

討論n維球面Sⁿ到自身連續映射的同倫類構成的集合[Sⁿ,Sⁿ]，是映射的同倫分類問題中最基本的內容，並且很多幾何問題的解決都有賴於對這個集合性質的了解。研究這個集合結構的一種方法，就是對每個連續映射f:Sⁿ→Sⁿ聯繫一個整數，即所謂布勞威爾度，它是由布勞威爾(Brouwer,L.E.J.)首先提出的。