基本介紹
- 中文名：同倫型不變性質
- 外文名：homotopy type invariance
- 領域：數學
- 學科：拓撲學
- 對象：拓撲空間
- 定義：相同同倫型的拓撲空間所共有性質
概念,拓撲學,同倫,同倫群,
概念
同倫型不變性質(homotopy type invariance)是拓撲學的一種重要不變性質。具有相同同倫型的拓撲空間所共有的性質稱為同倫型不變性質。因為同胚的拓撲空間一定是同倫等價的，所以同倫型不變性質一定是拓撲不變性質，但反之不一定成立。例如，3維閉球體D與3維歐氏空間R具有相同同倫型，但D是緊緻空間而R則不是。緊緻性是拓撲不變性質，但不是同倫型不變性質。在代數拓撲學中討論的性質，如同調群、同倫群等都是同倫型不變性質。
拓撲學
拓撲學是數學的一個分支。常常被形象地比喻但卻並不準確地說成是研究圖形在空間中連續形變下的不變性質。“互鎖”是三維封閉曲線的一個拓撲性質。我們不能在不切割其中之一的條件下把兩個互相扣結的橡皮圈分開 (切割，是一個不連續形變)。但如像康德 (Kant)著重指出的，即使直觀地來看，這種描述性的定義也是太狹獈。儘管在一付手套中，左手戴的那隻與右手戴的那隻沒有什麼根本不同，但在三維空間中卻無法把其中的一個經過連續形變變成另一個。進一步來說，也沒有什麼理由一定要把討論的範圍局限在三維空間之內，或者甚至是局限在必須要有維數的空間之內。對於一個一般的拓撲空間來講，所必須的只是一條： 即應該有一個關聯於它的閉性 (或者鄰域)的概念。從一個空間到另一空間的連續函式或者連續映射必須保持閉性。一個可逆(雙向) 的連續映射稱為同胚。拓撲學就是研究拓撲空間在同胚映射下保持不變的性質 (確實存在一個從三維空間到其自身之上的同胚映射，它把一隻右手手套映為一隻左手手套)。
一般拓撲學關心的是在一般的拓撲空間或稍微特殊一點的拓撲空間中圖形 (通常是任意的點集) 的性質。它所研究的是例如極限、連通性等概念。它的定理並不深入但卻有很廣的套用。
拓撲學中最有力最漂亮的定理是對於某些特殊的並可能還有一些附帶結構的拓撲空間中比較有限的圖形而得出的。因為，在這種情況下有可能建立某種構架或者複合形 (例如，用一個由三角形組成的網路去復蓋一個空間) 去表示 (在組合拓撲學中) 或者去逼近 (在代數拓撲學中) 這種圖形，從而可以在其上套用數值方法或代數方法。就像在解析幾何學中那樣，對幾何內涵的探索可以通過或多或少的常規計算來實現。(解析拓撲學企圖不藉助於代數而去尋求結果，這是反常的)。
同調論關係於邊緣的概念，例如三維空間中球的邊緣是它的二維球面，而二維球面的邊緣是零。邊緣運算元的這種規範性質亦可在純代數的構架內再現; 這就是同調代數的基本要素。同倫論關係於圖形和映射在連續形變下所保持的性質。
同倫
設f、g是拓撲空間X到Y的兩個連續映射，若存在連續映射H：X×I→Y使得：
H(x，0)=f(x)
H(x，1)=gx∈X
設X為拓撲空間，x0∈X，用Mn(X，x0)表示全體連續映射α：(
，
)→(X，x0)所成的集合，α和α′相對於I的同倫關係αα′是Mn(X，x0)上的一個等價關係，它把Mn(X，x0)的元素分成一些同倫等價類，用πn(X，x0)表示這些等價類所成的集合.定義映射α*β：(I，I)→(X，x0)，使得：
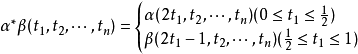
從而，α*β∈Mn(X，x0)，並且，若α∽α′，β∽β′，則：
因此，可在πn(X，x0)中定義運算：
