函式定義域,指該函式自變數的取值範圍,是函式的三要素之一。
基本介紹
- 中文名:函式定義域
- 外文名:Domain of a function
- 學科:數學
- 拼音:han shu ding yi yu
- 數學範疇:數學分析
函式
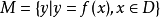
定義域
定義
分類

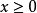
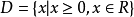
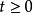
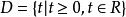

函式定義域,指該函式自變數的取值範圍,是函式的三要素之一。
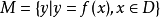

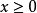
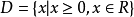
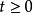
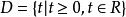
函式定義域,指該函式自變數的取值範圍,是函式的三要素之一。...... 函式定義域定義 在一個函式關係中,自變數x的取值範圍D叫作函式的定義域。 [1] ...
定義域(domain of definition)是函式三要素(定義域、值域、對應法則)之一,對應法則的作用對象。求函式定義域主要包括三種題型:抽象函式,一般函式,函式套用題。含義...
函式的定義:給定一個數集A,對A施加對應法則f,記作f(A),得到另一數集B,也就是B=f(A)。那么這個關係式就叫函式關係式,簡稱函式。函式概念含有三個要素:定義...
函式、三角函式和反三角函式經過有限次的有理運算(加、減、乘、除、有限次乘方、有限次開方)及有限次函式複合所產生、並且在定義域上能用一個方程式表示的函式。...
函式(function)表示每個輸入值對應唯一輸出值的一種對應關係。函式f中對應輸入值x的輸出值的標準符號為f(x)。包含某個函式所有的輸入值的集合被稱作這個函式的定義...
對A中的元素x施加對應法則f,記作f(x),得到另一數集B,假設B中的元素為y,則y與x之間的等量關係可以用y=f(x)表示,函式概念含有三個要素:定義域A、值域C和...
值域:數學名詞,函式經典定義中,因變數改變而改變的取值範圍叫做這個函式的值域,在函式現代定義中是指定義域中所有元素在某個對應法則下對應的所有的象所組成的集合...
反比例函式圖像 求用解析式表示的函式的定義域,就是求使函式各個組成部分有意義的集合的交集,對實際問題中函式關係定義域,還需要考慮實際問題的條件。 (2)值域與...
在建立函式關係時,首先要確定問題中的自變數與因變數,再根據它們之間的關係列出等式,得出函式關係式,然後確定函式定義域,確定定義域時,不僅要考慮到函式關係的解析式...
(1) 指數函式的定義域為R,這裡的前提是a大於0且不等於1。對於a不大於0的情況,則必然使得函式的定義域不連續,因此我們不予考慮,同時a等於0函式無意義一般也不...
一般地,對數函式以冪(真數)為自變數,指數為因變數,底數為常量的函式。對數函式是6類基本初等函式之一。其中對數的定義:如果ax=N(a>0,且a≠1),那么數x...
值與它對應的y值作為(x,y).在直角坐標系中作出的圖形叫正割函式的圖像,也叫...函式性質(1)定義域,x不能取90度,270度,-90度,-270度等值;即為{x|x≠k...
y=cosh x,定義域:R,值域:[1,+∞),偶函式,函式圖像是懸鏈線,最低點是(0,1),在Ⅰ象限部分是嚴格單調遞增曲線,函式圖像關於y軸對稱。...
“集合”和“對應”的概念給出了近代函式定義,通過集合概念把函式的對應關係、定義域及值域進一步具體化了,且打破了“變數是數”的極限,變數可以是數,也可以是...
函式列(sequence of functions)指各項為具有相同定義域的函式的序列。...... 函式列(sequence of functions)指各項為具有相同定義域的函式的序列。若{fn}為函式列,...
函式方程代換法 把函式方程中的自變數適當地以別的自變數代換(代換時應注意使函式的定義域不會發生變化),得到一個新的函式方程,然後設法求得未知函式...
函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係可以用y...
初等函式在其定義域內連續。一個初等函式,除了可以用初等解析式表示以外,往往還有其他表示形式。例如 ,三角函式 y=sinx 可以用無窮級數表為y=x-x3/3!+x5/5!...
函式的有界性是數學術語。設函式f(x)的定義域為D,f(x)在集合D上有定義。如果存在數K1,使得 f(x)≤K1對任意x∈D都成立,則稱函式f(x)在D上有上界。反...
