黎曼-施瓦茲對稱原理

簡介

黎曼-施瓦茲對稱原理是解析開拓的一種方法。

若D與D*為z平面上的兩個區域，它們關於實軸對稱，D位於上半平面，它們的邊界都包含實軸上一線段s。{D,f(z)}是一個解析元素，f(z)在D∪S上連續且在S上取實數值，則存在一個函式F(z)，滿足：

1.在區域D∪S∪D*內解析；

2.在D內有F(z)=f(z)；

3.在D*內有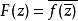

;

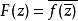
則稱

是{D,f(z)}的越過S的直接解析開拓。

解析元素亦稱解析函式元素，或簡稱函式元素，是單值解析函式及其定義域組成的二元組。

設D是複平面上的一個區域，f(z)是區域D內的單值解析函式，則函式f(z)和區域D的組合稱為一個解析元素，記為{D,f(z)}。

解析延拓是數學上將解析函式從較小定義域拓展到更大定義域的方法。透過此方法，一些原先發散的級數在新的定義域可具有迥異而有限的值。其中最知名的例子為Γ函式與黎曼ζ函式。

把解析函式的定義域擴大的過程。解析開拓通常有兩種方法，一種是利用冪級數進行解析開拓，這是外爾斯特拉斯的貢獻。他研究了解析函式用冪級數表示的問題。另一種解析開拓的方法是利用施瓦茲對稱原理，這是由德國數學家施瓦茲建立的把解析函式定義域作對稱擴大的解析開拓法。