泰希米勒空間,是指黎曼曲面復結構的形變所組成的空間。理論主要是用擬共形映射為工具來研究黎曼曲面的模問題,這種研究與克萊因群以及低維拓撲問題有一定的聯繫。
基本介紹
- 中文名:泰希米勒空間
- 外文名:Teichmuller space
- 概念:黎曼曲面復結構的形變組成的空間
- 發表時間:20世紀30年代末及40年代初
背景,黎曼曲面的模空間,發展,
背景
第一個給出黎曼曲面的模問題的實質進展的人是泰希米勒(O.Teichm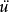 ller)。
ller)。
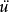
他在 20 世紀 30 年代末引進了 的一個覆蓋空間
的一個覆蓋空間 其中
其中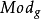 是一個間斷群,稱為模群(moduli group)。於是,他把問題轉化為對
是一個間斷群,稱為模群(moduli group)。於是,他把問題轉化為對 的研究,他運用擬共形映射理論,證明了
的研究,他運用擬共形映射理論,證明了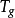 同胚於
同胚於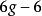 維歐幾里得空間中的單位球內部。
維歐幾里得空間中的單位球內部。


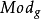

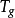
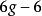
阿爾福斯(L.V.Ahlfors) 在20 世紀50年代進一步研究了 ,並稱之為泰希米勒空間。他證明了泰希米勒空間
,並稱之為泰希米勒空間。他證明了泰希米勒空間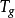 是
是 維的複流形,而其結構使
維的複流形,而其結構使 構為一個
構為一個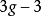 維的解析空間。
維的解析空間。

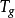


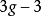
後來,貝爾斯 ( L.Bers) 進一步證明了 可以全純地嵌入
可以全純地嵌入 中,成為有界域。
中,成為有界域。


在阿爾福斯與貝爾斯的影響下,人們對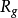 與
與 作了廣泛而深入的研究,而這種研究遠遠超出了複分析的範圍。
作了廣泛而深入的研究,而這種研究遠遠超出了複分析的範圍。
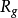

20 世紀 70 年代末,瑟斯頓(W.P.Thurston)建立了這種研究與低維拓撲的聯繫。
沙立文(D.Sullivan)則建立了它與復動力系統的聯繫,物理學家們同時發現了模空間在弦理論中的意義。
黎曼曲面的模空間
[moduli space of Riemann surface]
一個固定虧格的緊黎曼曲面的共形等價類的參數空間(parametric space)。
它源自黎曼在1857 年的一個猜想:全體虧格(genus)為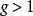 的黎曼曲面的共形等價類所組成的空間
的黎曼曲面的共形等價類所組成的空間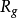 ,可以用
,可以用 個復參數全純描述。這裡用來代表黎曼曲面等價類參數,稱為它的模(modulus)。
個復參數全純描述。這裡用來代表黎曼曲面等價類參數,稱為它的模(modulus)。
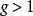
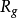

由黎曼曲面的黎曼-羅赫定理可以推出,虧格為零的緊黎曼曲面必然共形等價於黎曼球面。因此,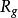 中只有一個元素。另外,由黎曼曲面的阿貝爾定理,可以推出任何一個虧格為 1 的黎曼曲面共形等價於
中只有一個元素。另外,由黎曼曲面的阿貝爾定理,可以推出任何一個虧格為 1 的黎曼曲面共形等價於 其中
其中 是一個虛部大於零的複數,而
是一個虛部大於零的複數,而 是一個由
是一個由 確定的格群
確定的格群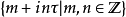 。根據這一結果,人們不難將
。根據這一結果,人們不難將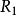 的參數空間取為
的參數空間取為 .其中 U 為上半平面,而Mod為模變換群(moduli transformation group)。
.其中 U 為上半平面,而Mod為模變換群(moduli transformation group)。
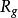




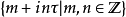
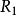

這樣,唯獨只有g > 1的情形, 的參數化問題成為一大難題,這就是著名的黎曼曲面的模問題。
的參數化問題成為一大難題,這就是著名的黎曼曲面的模問題。

發展
對於泰希米勒空間的研究導致了萬有泰希米勒空間的概念。所謂萬有泰希米勒空間實際上是指滿足規範條件的在單位圓內單葉解析而在單位圓外能擬共形開拓的函式所組成的空間。
對於泰希米勒空間的邊界的研究導致了對邊界群的探討。這是一類特殊的克萊因群,它只有一個單連通的不變分支。此外,W.P.瑟斯頓基於他對曲面葉狀結構的研究,給出了空間Tg的一種緊化,並在此基礎上證明了關於緊曲面上保向自同胚的分類定理。
伯斯給瑟斯頓定理以分析的證明,並相應地給出了模群元素的分類。

