泰希米勒形變

拓撲曲面S_g上的全純坐標產生一個黎曼曲面S'_g及泰希米勒空間的一個點[S'_g,T]，其中T:S_g→S'_g作為拓撲曲面S_g上的自同胚為恆等映射，T及[S'_g,T]稱為泰希米勒形變。

基本介紹

• 中文名：泰希米勒形變
• 外文名：Teichmüller deformation
• 適用範圍：數理科學

簡介

設0<k<1，ζ是S_g上某一非零全純二次微分w誘導的自然參數，令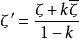，易知ζ'滿足局部坐標的相容性條件，因而參可作為拓撲曲面S_g上的全純坐標。

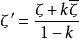
由此產生一個黎曼曲面S'_g及泰希米勒空間的一個點[S'_g,T]，其中T:S_g→S'_g作為拓撲曲面S_g上的自同胚為恆等映射，T及[S'_g,T]稱為泰希米勒形變。

全純二次微分

全純二次微分是一種特殊的二次微分式，是在局部坐標z下表為w=f(z)dz²且在局部坐標變換下不變的微分式。若f是點z的全純函式，則稱w為S_g上的全純二次微分式。

由黎曼-羅赫定理可知：Sg上所有全純二次微分的全體是6g-6維實的向量空間。

泰希米勒空間

泰希米勒空間，是指黎曼曲面復結構的形變所組成的空間。理論主要是用擬共形映射為工具來研究黎曼曲面的模問題，這種研究與克萊因群以及低維拓撲問題有一定的聯繫。