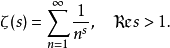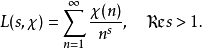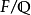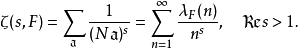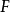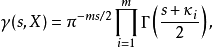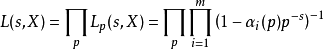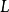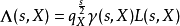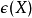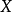簡介
數論中以分析方法作為研究工具的一個分支。分析方法在數論中的套用可以追溯到18世紀L.
歐拉的時代。歐拉證明了,對實變數s>1有
恆等式 (式中s取遍所有素數)成立,並且由此推出素數有無窮多個。
歐拉恆等式是數論中最主要的定理之一。隨後P.G.L.
狄利克雷創立了研究數論問題的兩個重要工具,即狄利克雷(剩餘)
特徵標與狄利克雷L函式,奠定了解析數論的基礎。
聯繫
數論和
複變函數論的橋樑是所謂的佩隆公式(Peron)。很多數論問題可以歸結為某類求和函式的估計問題,而利用佩隆公式,就可以將求和函式的估計轉變為某類
複變函數的
零點、
極點的分布情況的估計。 大多數數論問題最終都能歸結為L函式的性質討論。
令π(x)表示不超過x的素數的個數,關於π(x)的研究是素數論的中心問題,
黎曼在數論中引入複變函數ζ(s),稱為黎曼ζ函式(見數論),他對這個函式作了深入的研究,得到了許多重要結果。特別是 ,他建立了一個與ζ(s)的零點有關的表示π(x)的公式,因此研究
素數分布問題的關鍵在於研究ζ(s)的性質特別是它的零點的性質。這樣,黎曼開創了解析
數論的一個新時期。黎曼提出一個猜想:ζ(s)的所有復
零點都在直線Res=1/2上,這就是所謂
黎曼猜想。它是尚未解決的最著名的數學問題之一。
1896年,J.
阿達馬與C.J.dela瓦萊-普桑用解析方法同時並且相互獨立地證明了
素數定理即當x→∞時,π(x)~.x/lnx (這個問題最早由
高斯提出),從此解析數論開始得到迅速發展。1949年,A.
塞爾伯格與P.愛爾特希分別給出了對於素數定理的一個十分初等的分析證明,當然它是很複雜的。
解析數論的基礎
歐拉恆等式是
數論中最重要的定理之一,是
算術基本定理的解析
等價形式,揭示了素數
p和自然數
n之間的積性關係。他還提出了
母函式法,利用
冪級數來研究
整數分拆,這導致圓法和指數和方法的產生。其後,P.G.L.狄利克雷套用分析方法於1837年解決了首項與公差互素的
算術級數中有無限多個素數的問題,又於1839年推證出
二次域的
類數公式。他創立了研究數論的兩個重要工具,即
狄利克雷(剩餘)特徵標與狄利克雷
l函式,奠定了解析數論的基礎。
1859年,(G.F.)B.黎曼發表了一篇關於不大於
x的
素數個數
π(
x)的著名論文《論不大於一個給定值的素數個數》,這是他在
數論方面公開發表的惟一的文章。他把
恆等式的右邊的
級數記作
ζ(
s),所不同之處是把
s看作復變數。現在稱
ζ(
s)為
黎曼ζ函式。他認為素數性質可以通過
複變函數ζ(
s)來探討,並對複變函數
ζ(
s)做了深刻的研究,得到許多重要結果。特別是他建立了一個與
ζ(
s)的
零點有關的表示
π(
x)的公式。因此研究
素數分布的關鍵在於研究複變函數
ζ(
s)的性質,特別是
ζ(
s)的零點性質。這一傑出的工作,是
複變函數論的思想和方法套用於數論研究的結果。
黎曼開創了解析
數論的新時期,也推動了單複變函數論的發展。在文章中他提出了一個猜想:
ζ(
s)的所有復零點都在直線 Re
s=1/2上。這就是所謂
黎曼猜想。它是至今沒有解決的最著名的數學問題之一。它的研究對解析數論和
代數數論的發展都有極其深刻的影響。
解析數論的發展
1896年,J.(-S.)阿達馬與C.de la瓦萊-普桑嚴格地按照
黎曼提出的方法和結果,用
整函式理論,同時證明了
素數定理:當
x→∞時,
π(
x)~
x(ln
x)-1。從此解析數論開始得到迅速發展,而在此以前的30年中卻無顯著進展。 在
數論中套用分析方法,大致有兩種情況:一是數論問題本身不涉及分析概念。這類問題又可分為兩種情形,或者有一些問題不套用分析方法就不能解決,例如,上述的
狄利克雷的兩個工作、三素數定理(見數論、
堆壘數論)、
華林問題;或者有一些問題套用分析方法可使證明簡單、可以對問題做
定量研究,例如,套用
母函式法對
整數分拆的一些
恆等式的證明、
歐拉證明素數有無窮多個的分析方法導致H.默滕斯證明了關於素數平均分布的三個定理、堆壘數論的許多問題引入分析方法證明解的存在性,得出解數的漸近公式或上下界估計。二是
數論問題本身必須用分析概念才能表達清楚。例如,關於
素數定理,即不大於
x的素數個數
π(
x)等於多少的問題(見
素數分布)。此外,利用分析概念還可提出新的數論問題,例如各種
數論函式的階估計及
均值估計(見
格點問題)。
 解析數論
解析數論解決一個數論問題需要用到多深的分析工具,或者能否不用分析工具。這也是數學家努力為之探索的問題。例如,在1949年A.賽爾伯格與P.愛爾特希不利用
ζ函式,且除了
極限、e
x和lnx的性質外,也不需要其他的分析知識,給出了
素數定理一個十分初等的分析證明。當然它是很複雜的。
解析數論兩大問題
解析數論,一直以來有兩大問題,素數方程與L-函式。
素數方程
素數,即我們中國小學到的質數,從乘法角度講,相當於構成整數的“原子”。Goldbach猜想,即是一種素數方程問題,即方程的解集在素數
集合里考慮。
Fields獎得主Bombieri在大篩法方面做出了重要工作,從而給陳景潤等一批中國數學家帶來機會,先是潘承洞解決了1+5型問題,王元解決2+3型的同時構造出了後續攻擊路線的解決框架,包括1+4和1+3,最後由陳景潤解決了1+2型問題,一直到現在都無法改進,是中國數學家目前為止最拿得響的工作,因為目前誰也做不出最難的1+1型。
素數方程方面,1998年Fields獎得主Gowers獲獎之後,緊接著在
整數方程做出了開創性的工作,然後由Terence Tao(陶哲軒)和Ben Green推廣到素數方程方面,這個推廣,很不平凡,陶哲軒獲得了2006年Fields獎。
Gowers-Tao-Green的思想,將素數方程做了系統的突破,可以解決絕大多數的線性方程組問題,唯獨不能攻擊Goldbach猜想。
素數方程方面,一直以來有兩大方法:篩法和圓法。前者自古希臘時期就被發現,陳景潤的工作,就是動用此法。圓法,則是英國劍橋的Hardy-Littlewood-Ramanujan發明,至今也套用了90多年了。
Gowers-Tao-Green,其價值地位相當於第三種方法出世,正是因為增加了新的理解,才有可能得到新的突破性結果。Gowers-Tao-Green增加的是哪種新思想,這種新思想,除了素數方程的數論問題之外,亦很可能對其他數學領域也產生深刻影響。
經典解析數論在素數方程方面的研究思路是:
A-Step 1. Summation Formulas (各種求和公式)
A-Step 2. Equations Detect (方程探測)
L-函式
一般地說,
-函式來源由兩類組成:算術L-函式和自守L-函式。這兩者又是密切聯繫在一起的,根據
羅伯特·朗蘭茲的猜想,籠統地說, 一切有意義的L-函式都來自自守L-函式。
算術L-函式
簡單地說,
同樣地,
狄利克雷在研究
算術級數中的素數分布時,引入了Dirichlet L-函式:
Dedekind zeta-函式:設
為一代數
數域,
橢圓曲線的Haass-Weil L-函式:設
為一非奇異的橢圓曲線
定義
為曲線在
有限域 上的解,設
,則下面的級數稱為關於曲線的Haass-Weil L-函式
阿廷L-函式:設
是一個有限維的伽羅瓦表示,其中
為一代數數域,
自守L-函式
全純模形式的L-函式,Maass L-函式,標準L-函式等等。
研究內容
根據羅伯特·朗蘭茲在國際數學家大會上的報告所指,研究一個L-函式主要有三部分內容:
1.解析延拓
L-函式的解析延拓和函式方程這是最基本的一部分。對於一般的自守L-函式這是較容易得到的, 但是對算術的L-函式這一部分並不是容易得到的。例如,對於Haass-Weil L-函式,這部分就是谷山-志村猜想,該猜想一部分就能推出
費爾馬大定理。關於阿廷L-函式的全純解析沿拓的阿廷猜想也是數論中重要的未知問題。
對於數學對象
的L-函式,我們定義其的gamma因子為
那么,一般地我們有函式方程
2.零點的分布
非零區域:如黎曼zeta函式的目前最好的非零區域為
在假設黎曼猜想下,零點虛部的分布問題與隨機矩陣的聯繫等等。
3.特殊點的值
中心值,臨界點,整點的值,
極點的留數等。這裡面也有很多猜想,像BSD猜想,類數問題,Deligne 猜想,Beilinson 猜想,Goldfeld猜想。其實往往我們重要的不僅是關心它具體有多大,而是關心的這個量裡面隱含著什麼樣的算術意義。像Dedekind zeta 函式在s=1處的留數,裡面包含了一個數域的很多不變數:類數,判別式,regular等;BSD猜想就是Haass-Weil L-函式在中心點的的階就是該橢圓曲線的秩!
 解析數論
解析數論
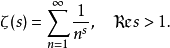
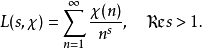
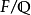
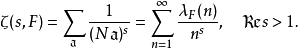

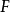


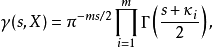

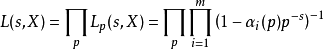

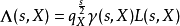

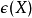

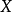


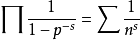
 解析數論
解析數論