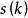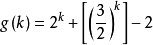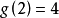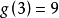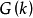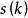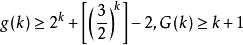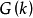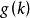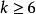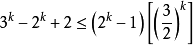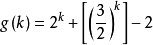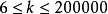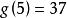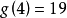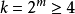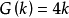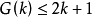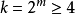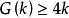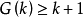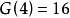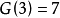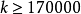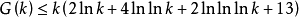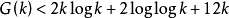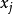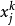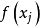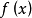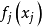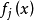基本介紹
- 中文名:加性數論
- 外文名:additive theory of number
- 別名:堆壘數論
- 相關問題:加性問題
- 著名問題:哥德巴赫猜想、華林問題等
- 所屬學科:數學(解析數論)
基本介紹,多角數問題,平方和問題,哥德巴赫問題,華林問題,
基本介紹
加性數論(additive theory ofnumber) 又稱堆壘數論,是關於“加性問題”的一個數論分支。它研究的典型問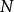 題是:設
題是:設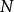 是全體非負整數的集合,
是全體非負整數的集合,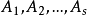 是的有限個或可數個子集,試判定對
是的有限個或可數個子集,試判定對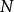 中的每一個n,方程
中的每一個n,方程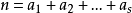 是否可解或其解數
是否可解或其解數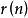 ,其中
,其中 。這類問題與整數集合的加法性質有關。堆壘數論的歷史也很古老,費馬等人就開始了堆壘數論的某些研究。以下是幾個著名的堆壘數論問題。
。這類問題與整數集合的加法性質有關。堆壘數論的歷史也很古老,費馬等人就開始了堆壘數論的某些研究。以下是幾個著名的堆壘數論問題。
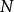
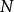
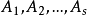
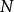
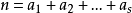
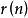

多角數問題
設整數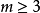 ,由
,由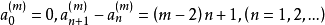 確定——個數列
確定——個數列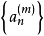 ,屬於這個數列的整數稱為m階多角數。其通項為:
,屬於這個數列的整數稱為m階多角數。其通項為: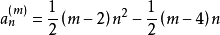 。易知,4角數就是平方數。1636年,費馬猜測:每個自然數都可以表示為m個m階多角數之和。拉格朗日於1772年證明了m=4的情況;勒讓德於1798年證明了m=3的情況;1813年,柯西證明了,這個猜測,解決了多角數問題。
。易知,4角數就是平方數。1636年,費馬猜測:每個自然數都可以表示為m個m階多角數之和。拉格朗日於1772年證明了m=4的情況;勒讓德於1798年證明了m=3的情況;1813年,柯西證明了,這個猜測,解決了多角數問題。
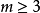
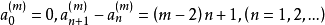
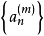
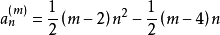
平方和問題
求不定方程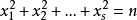 的整數解的個數
的整數解的個數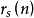 的問題,其中s是給定的正整數。例如
的問題,其中s是給定的正整數。例如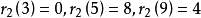 。
。
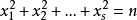
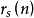
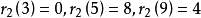
1829年,雅可比對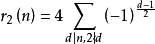 予以證明,還證明了
予以證明,還證明了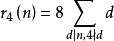 。1919年,哈代等人得到了
。1919年,哈代等人得到了 時,
時,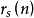 的漸近公式。現在對s≤24,均已得出
的漸近公式。現在對s≤24,均已得出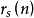 的具體表達式。1926年克洛斯特曼,1962年埃斯特曼分別討論了形如
的具體表達式。1926年克洛斯特曼,1962年埃斯特曼分別討論了形如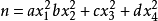 的平方和問題,拓廣了平方和問題,開拓了一系列新的領域。
的平方和問題,拓廣了平方和問題,開拓了一系列新的領域。
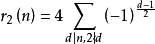
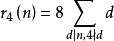

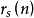
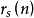
哥德巴赫問題
哥德巴赫問題是堆壘數論亦是整個數論最有魅力的問題之一(見哥德巴赫猜想)。
華林問題
1770年,華林推測:任意正整數能夠用不超過4個平方數的和、不超過9個立方數之和或不超過19個四次方數之和來表示。意思是:對任意給定的整數k≥2,必存在一個正整數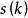 ,使得每個正整數n必是
,使得每個正整數n必是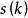 個非負的k次方數之和。即不定方程
個非負的k次方數之和。即不定方程
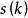
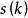
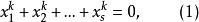
對所有的整數n≥0有非負整數解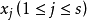 。這就是華林問題(還包括解的數目及極值問題)。
。這就是華林問題(還包括解的數目及極值問題)。
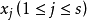
華林還猜測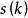 的最小值
的最小值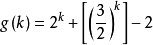 。1770年拉格朗日證明了
。1770年拉格朗日證明了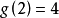 ;1909年威弗里奇證明了
;1909年威弗里奇證明了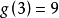 。設
。設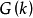 為使方程(1)對充分大的n可解的
為使方程(1)對充分大的n可解的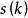 的最小值,易證
的最小值,易證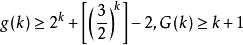 。利用
。利用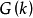 的上界估計,人們基本上完成了對
的上界估計,人們基本上完成了對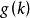 的探討:當
的探討:當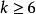 時有條件
時有條件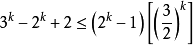 時,
時,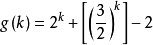 。1957年,馬勒爾證明當k充分大時條件一定成立;1964年,斯泰姆勒爾證明此條件存
。1957年,馬勒爾證明當k充分大時條件一定成立;1964年,斯泰姆勒爾證明此條件存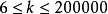 時成立。1964年陳景潤證明
時成立。1964年陳景潤證明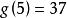 ;1985年巴拉薩布雷尼安等證明了
;1985年巴拉薩布雷尼安等證明了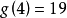 。
。