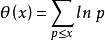素數分布是數論中研究素數性質的重要課題。素數或稱質數，是指一個大於1的整數，除1和它本身外，不能被其他的正整數所整除。研究各種各樣的素數分布狀況，一直是數論中最重要和最有吸引力的中心問題之一。關於素數分布性質，通過數值觀察、計算和初步研究發現，素數分布是以黎曼公式為中心，高斯公式為上限的常態分配，這在現在來說是經驗公式，待數學家給出嚴格證明之後才能成為數學定理。
基本介紹
- 中文名：素數分布
- 外文名：distribution of prime numbers
- 性質：素數的分布越往上越稀少
- 作用：數論中研究素數性質
- 時間：公元前300年
- 本質：常態分配
歷史,分布規律,分類,變化,證實疑雲,素數分布逼近函式公式,著名的素數分布猜想,孿生素數猜想,梅森素數分布,素數定理,算術級數中的最小素數,相鄰素數之差,
歷史
分布規律
將自然數劃分成6（6N2+6N)為界的一個個區間，就出現了素數分布規律，各區間的素數，以波浪形式漸漸增多，只有個別的區間比前面的少，造成這種現象的原因是，有性合數的因子多少和素數對區間的不整除之故。
以下10個區間統計數據，
S1區間1——72，有素數18個，孿生素數7對。（2和3不計算在內，最後的數是孿中的也算一對）
S2區間73——216，有素數27個，孿生素數7對。
S3區間217——432，有素數34個，孿生素數8對。
S4區間433——720，有素數45個，孿生素數7對。
S5區間721——1080，有素數52個，孿生素數9對。
S6區間1081——1512，素數51個，孿生素數9對。
S7區間1513——2016，素數63個，孿生素數10對。
S8區間2017——2592，素數71個，孿生素數13對。
S9區間2593——3240，素數78個，孿生素數11對。
S10區間3241——3960，素數91個，孿生素數19對。
S11區間3961——4752素數92個，孿生素數17對。
S12區間4752——5616素數98個，孿生素數13對。
S13區間5617——6552素數108個，孿生素數14對。
S14區間6553——7560素數113個，孿生素數19對。
S15區間7561——8640素數116個，孿生素數14對。
大約在公元前300年,歐幾里得就證明了素數有無窮多個。設2,3,…,p是不大於p的所有素數，q=2*3*…*p+1。容易看出q不是2，3，…，p的倍數。由於q的最小正除數一定是素數，因此，或者q本身是一個素數，或者q可被p與q之間的某兩個素數所整除[比如：2*3*5*7*11*13+1=30031=59*509]。所以必有大於p的素數存在，由此即知素數有無窮多個。
分類
素數可分成陰性素數（6N-1)，陽性素數（6N+1）和起碼素數（1，2，3）.
研究素數可以按照個位分為4類：個位分別是1、3、7、9（不包括素數2和素數5這兩個特殊素數）。
比如個位為3的素數是：03、13、23、43、53、73、83、103.......。這樣的分類的好處是可以更好的探索素數的產生過程；素數研究相對簡單化；可以去掉個位來研究。
下表是大約107億以內的個位為3的素數分布情況，可以看到自然數增加一倍，素數個數增加也越來越接近一倍。當自然數趨向無窮時，其應與自然數增長比率相同。
自然數（表中數字去掉個位9後，實際上是逐行翻倍） | 素數的個位為3 | |
累計素數個數 | 倍增比值 | |
19 | 2 | |
29 | 3 | 1.5 |
49 | 4 | 1.333333333 |
89 | 7 | 1.75 |
169 | 10 | 1.428571429 |
329 | 18 | 1.8 |
649 | 30 | 1.666666667 |
1289 | 54 | 1.8 |
2569 | 97 | 1.796296296 |
5129 | 175 | 1.804123711 |
10249 | 317 | 1.811428571 |
20489 | 583 | 1.839116719 |
40969 | 1086 | 1.862778731 |
81929 | 2002 | 1.843462247 |
163849 | 3755 | 1.875624376 |
327689 | 7071 | 1.883089214 |
655369 | 13338 | 1.886296139 |
1310729 | 25209 | 1.890013495 |
2621449 | 47851 | 1.898171288 |
5242889 | 91110 | 1.904035443 |
10485769 | 173756 | 1.907101306 |
20971529 | 332201 | 1.91188218 |
41943049 | 636108 | 1.914828673 |
83886089 | 1220765 | 1.919115936 |
167772169 | 2346530 | 1.922179945 |
335544329 | 4517428 | 1.925152459 |
671088649 | 8707822 | 1.927606151 |
1342177289 | 16810346 | 1.930488014 |
2684354569 | 32487852 | 1.932610548 |
5368709129 | 62859510 | 1.934861991 |
10737418249 | 121757490 | 1.936978032 |
結論：素數將與自然數一樣無限增長。 | ||
自然數增加1倍後，素數增長趨勢是：逐漸也增加1倍。 | ||
自然數趨向無窮大後，自然數增加1倍，孿生素數也應增加1倍。 | ||
變化
素數在自然數中占有極其重要的地位，但是它的變化非常不規則。人們至今沒有找到，大概也不可能找到一個可以表示全體素數的有用公式。最初的研究方法，是通過觀察素數表來發現素數分布的性質。現有的較完善的素數表是D.B.扎蓋爾於1977年編制的，列出了不大於50000000的所有素數。從素數表可以看出：在1到100中間有25個素數,在1到1000中間有168個素數,在1000到2000中間有135個素數, 在2000到3000中間有127個素數，在3000到4000中間有120個素數,在4000到5000中間有119個素數,在5000到10000中間有560個素數。由此可看出，素數的分布越往上越稀少。
36N（N+1）±1都是素數的，這樣的孿生素數有很多，並且是無限多的。
雁盪山孿生素數[36N（N+1）±1]，在N=100000000以內有109128對，
證實疑雲
據《人民網》轉載英國《每日郵報》報導：2015年11月，奈及利亞教授奧派耶米 伊諾克(Opeyemi Enoch)成功解決已存在156年的數學難題——黎曼猜想，獲得100萬美元(約合人民幣630萬元)的獎金。
該新聞已被證偽。
素數分布逼近函式公式
x為素數排列後的位置序號，p 為對應的素數，則素數分布公式如下：
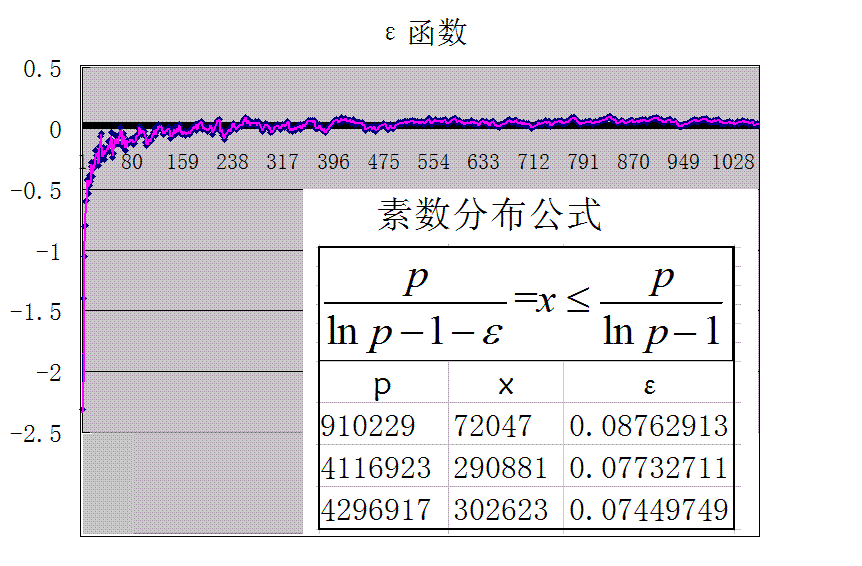圖1 ε函式ε在x=72047處為最大值，x增加時，ε逐步減小，當x趨於無窮大時，ε應該趨於0。此公式是4296917以內的不完全逼近公式。公式比較客觀有效。
素數分布與平方數
的關係
所有素數都在完全平方數的周期以內，理論上是可以通過完全平方數來尋找素數，以下是基於此我們發現以下三組數據距離素數很近，
稱為完全平方分解數，是由偶奇比函式歸納出來的。
素數距離這三組數據最近，如果三組中均無素數，那么就在Sn1及Sn2之外，以下是素數距離Sn0的振幅函式
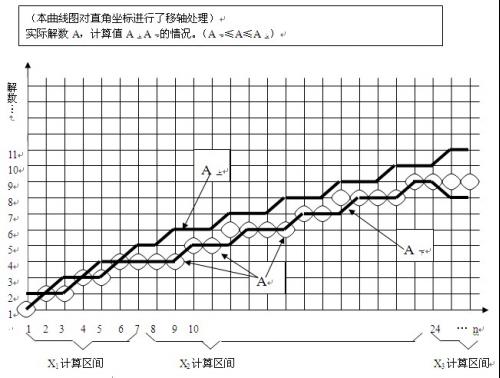
圖2中值圖像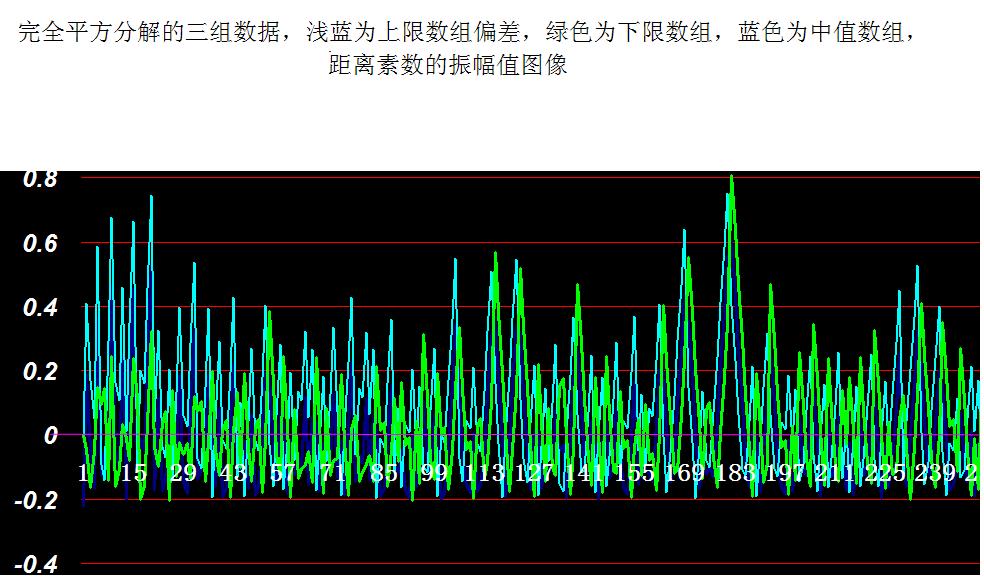
圖3 3組數據對比圖左圖是中值Sn0的圖像，右圖是三組合併一起的對比圖，這是素數分布最為核心的規律，素數分布，以中值下偏幾率最大，上偏的比較稀少。所謂素數常態分配應該是以完全平方分解數為中心的。。而且稍微下偏才是分布的峰值線。。具體由振幅函式見證。
著名的素數分布猜想
孿生素數猜想
兩個差等於2的一對素數,稱為孿生素數。例如,3和5；5和7；11和13；17和19；29和31；41和43；59和61；71和73；101和103；…10016957和10016959；都是孿生素數。迄今所知的最大孿生素數是1159142985×2-1和1159142985×2+1；它們是A.O.L.阿特金和N.W.里克特於1979年得到的。
所謂孿生素數猜想，即存在無窮多對孿生素數。這個猜想至今沒有解決，但認為它是正確的可能性很大。在這方面的最好結果是中國數學家陳景潤於1966年得到的：存在無窮多個素數p，使得p+2是不超過兩個素數之積。
梅森素數分布
2^P-1型的數稱為梅森數，並以Mp記之；而 2^P-1型的素數稱為梅森素數。這種特殊素數貌似簡單，但探究難度卻極大。它不僅需要高深的理論和純熟的技巧，而且還需要進行艱巨的計算。梅森素數歷來是數論研究的一項重要內容，也是當今科學探索的熱點和難點之一。2013年2月6日，據英國《新科學家》雜誌網站報導，柯蒂斯·庫珀(Curtis Cooper)領導的研究小組於1月25日日發現了已知的最大梅森素數--“2^57885161-1”，該素數有17,425,170位，它是目前已知的最大素數。如果用普通字號將這個巨數連續寫下來，其長度可超過65公里！迄今人們已經發現48個梅森素數。
梅森素數貌似簡單，但當指數P值較大時，其探究難度就會很大。例如：1772年，有“數學英雄”美名的瑞士數學大師歐拉在雙目失明的情況下，靠心算證明了2^31-1(即2147483647)是第8個梅森素數。這個具有10位的素數，堪稱當時世界上已知的最大素數。在“手算筆錄”的年代，人們僅找到12個梅森素數。而計算機的誕生和格線技術的出現，加速了梅森素數探究的進程。1996年初，美國數學家、程式設計師喬治·沃特曼編制了一個梅森素數計算程式，並把它放在網頁上供全球數學家和業餘數學愛好者免費使用。它就是舉世聞名的GIMPS項目。
為了激勵人們尋找梅森素數和促進格線技術發展，總部設在美國的電子新領域基金會（EFF）於1999年設立了專項獎金懸賞參與GIMPS項目的梅森素數發現者。它規定向第一個找到超過100萬位數的個人或機構頒發5萬美元。後面的獎金依次為：超過1000萬位數，10萬美元；超過1億位數，15萬美元；超過10億位數，25萬美元。不過，絕大多數人參與該項目並不是為了金錢，而是出於好奇心、求知慾和榮譽感。
梅森素數的分布極不規則。探索梅森素數的分布規律似乎比尋找新的梅森素數更為困難。數學家們在長期的摸索中，提出了一些猜想。英國數學家香克斯、美國數學家吉里斯、法國數學家托洛塔和德國數學家伯利哈特就曾分別給出過關於梅森素數分布的猜測，但他們的猜測有一個共同點，就是都以近似表達式給出；而它們與實際情況的接近程度均未盡如人意。中國數學家及語言學家周海中經過多年的研究，於1992年首次給出了梅森素數分布的精確表達式，為人們尋找這一素數提供了方便；後來這一重大成果被國際上命名為“周氏猜測”。該猜測的內容為：當2^(2^n)<p<2^(2^(n+1))時，Mp有2^(n+1)-1個是素數（註：p為素數；n為自然數；Mp為梅森數）。美籍挪威數論大師、菲爾茨獎和沃爾夫獎得主阿特勒·塞爾伯格認為：周氏猜測具有創新性，開創了富於啟發性的新方法；其創新性還表現在揭示新的規律上。
計算梅森素數個數的公式，3*5/3.8*7/5.8*11/9.8*13/11.8*......*P/(P-1.2)-1=M
P是梅森數的指數，M是P以下的梅森素數的個數。
指數5，計算2.947，實際3 ，誤差0.053；
指數7，計算3.764，實際4 ，誤差 0.236；
指數13，計算4.891，實際5，誤差0.109；
指數17，計算5.339，實際6，誤差0.661；
指數19，計算5.766，實際7，誤差1.234；
指數31，計算6.746，實際8，誤差1.254；
指數61，計算8.445，實際9，誤差0.555；
指數89，計算9.201，實際10，誤差0.799；
指數107，計算9.697，實際11，誤差1.303；
指數127，計算10.036 ，實際12，誤差1.964；
指數521，計算13.818，實際13，誤差-0.818；
指數607，計算14.259，實際14，誤差-0.259；
指數1279，計算16.306，實際15，誤差-1.306；
指數2203，計算17.573，實際16，誤差-1.573；
指數2281，計算17.941，實際17，誤差-0.941；
素數定理
關於素數個數的研究是素數分布中最重要的問題之一。以 π(x)表示不大於x的素數個數，例如，π(2)=1，π(3)=2，π(100)=25，π(1000)=168。歐幾里得早就證明了素數有無窮多個，即。從表可以看出：①x越大,π(x)與x的比值越接近於0；②x越大,π(x)與x/lnx的比值越接近於1。A.-M.勒讓德和C.F.高斯猜測即通常所稱的素數定理。它是素數分布理論的中心定理。在這方面首先做出貢獻的是∏.Л.切比雪夫，他在1852年左右證明了存在兩個正常數с1,с2，使得不等式с1x/lnx≤π(x)≤с2x/lnx成立，其中x≥2。在1896年，J.（-S.）阿達馬和C.瓦萊·普桑彼此獨立而又幾乎同時證明了素數定理。他們的證明都使用了高深的複變函數論知識。因此，能否以儘可能初等的方法來證明素數定理，則成為數學家一直探討的重要問題。1949年，A.賽爾伯格和P.愛爾特希給出了素數定理的初等證明，除了極限、lnx和e的性質之外，沒有用到其他的分析知識，但證明過程十分複雜。他們的證明是基於賽爾伯格的著名恆等式：
當x≥1時有
式中
，
表示對所有不超過x的素數求和，記號O的定義如下：設g(x)>0,ƒ(x)為一復值函式, α≤x≤b)。若存在一個與x無關的正常數M,使得當α≤x≤b)時有|ƒ(x)|≤Mg(x),則記為ƒ(x)=O(g(x)),M稱為記號O所含之常數。於是某一滿足上述條件的函式ƒ(x),就可用O(g(x))代之。
有誤差項的素數定理是指尋求誤差π(x)-lix的最佳估計,,它比x/lnx更接近於π(x)。C.瓦萊·普桑於1900年首先證明了這裡с是一正的常數。H.von科赫於1901年在黎曼假設（見黎曼ζ函式）下證明了
O(xlnx)。
И.М.維諾格拉多夫等於1958年藉助於他的三角和估計方法,得到π(x)-lix=O(xexp(-с(lnx)))，ε為任意正數，с是和ε有關的正常數。誤差項π(x)-lix的變化是極不規則的。設ƒ(x)是實函式，如果存在與x無關的正常數α，使得任意大的x滿足ƒ(x)>αx，則記為ƒ(x)=Ω(x)；若使得任意大的x滿足ƒ(x)<- αx，則記為ƒ(x)=Ω-(x)。若這兩種情形同時出現，則記為ƒ(x)=Ω(x)。J.E.李特爾伍德於1914年證明了：當x→∞時，有π(x)-lix=Ω((xlnlnlnx)/lnx)。
式中с為絕對正常數；記號O中所含的常數僅與h有關，而與q無關。
算術級數中的最小素數
設k≥3，1≤l≤k，(l,k)=1。以p(k,l)表算術級數knl(n=0,1,2,…)中的最小素數。S.喬拉猜測p(k,l)=O(k)，其中ε為任意小的正數。ю.Β.林尼克於1944年首先證明了存在絕對常數с，使得p(k,l)=O(k)。潘承洞於1957年首先指出с是可以計算的，並定出了с的值。目前最好的結果с≤17是陳景潤於1979年得到的。
相鄰素數之差
設pn是第n個素數，是相鄰的兩個素數之差。在黎曼假設下,H.克拉默於1921年證明了 無條件結果 是赫斯－布朗和H.伊瓦尼克於1979年得到的。另一方面，關於dn的下界，E.邦別里和H.達文波特於1966年證明了：M.N.赫胥黎於1977年改進為E≤0.4425。猜測應有E=0。關於dn還有許多有趣的研究。
