公式介紹 上下素性判定法
首先,本文英文字母都表示整數,上半部B 》3N 》W,下半部B 》W 》3N。大於3的素數只有6N-1和6N+1兩種形式,我們只需判定這兩種數是素數還是合數即可。
命題 1 對於B=36N+1 形數而言。
若不定方程(3N)^2+N-(B-1)/36=W^2 有整數解,
則 6(3N-W)+1 是小因子數;6(3N+W)+1 是大因子數。
若不定方程 (3N)^2-N-(B-1)/36=W^2 有整數解,
則 6(3N-W)-1 是小因子數;6(3N+W)-1 是大因子數。
兩式都無解,是素數。
命題 2對於B=36N+7 形數而言。
若不定方 (3N)^2+4N-(B-7)/36=W^2+W 有整數解,
則 6(3N-W)+1 是小因子數,6(3N+W+1)+1 是大因子數。
若不定方程 (3N+2)^2+2N+2-(B+29)/36=W^2+W 有整數解,
則 6(3N+2-W)-1 是小因子數,6(3N+W+3)-1 是大因子數。
兩式都無解,是素數。
命題 3對於B=36N+13 形數而言。
若不定方程 (3N+1)^2+N-(B-13)/36=W^2 有整數解,
則 6(3N+1-W)+1 是小因子數,6(3N+1+W)+1是大因子數。
若不定方程 (3N+2)^2-N-(B+23)/36=W2 有整數解,
則 6(3N+2-W)-1 是小因子數,6(3N+2+W)-1是大因子數。
兩式都無解,是素數。
命題 4 對於B=36N+19 形數而言。
若不定方程(3N+1)^2+4N+1-(B-19)/36=W^2 +W 有整數解,
則 6(3N+1-W)+1 是小因子數;6(3N+2+W)+1 是大因子數。
若不定方程 (3N+1)^2+2N+1-(B+17)/36=W^2 +W 有整數解,
則 6(3N+1-W)-1 是小因子數;6(3N+2+W)-1 是大因子數。
兩式都無解,是素數。
命題 5 對於B=36N+25 形數而言。
若不定方 (3N+2)^2+N-(B-25)/36=W^2有整數解,
則 6(3N+2-W)+1 是小因子數,6(3N+2+W)+1 是大因子數。
若不定方程 (3N+1)^2-N-(B+11)/36=W^2有整數解,
則 6(3N+1-W)-1 是小因子數,6(3N+1+W)-1 是大因子數。
兩式都無解,是素數。
命題 6 對於B=36N+31 形數而言。
若不定方程 (3N+2)^2+4N+2-(B-31)/36=W^2 +W 有整數解,
則 6(3N+2-W)+1 是小因子數,6(3N+3+W)+1是大因子數。
若不定方程 (3N+1)^2-4N-1-(B+5)/36=W^2+W有整數解,
則 6(3N-W)-1 是小因子數,6(3N+1+W)-1是大因子數。
兩式都無解,是素數。
命題 7對於B=36N-1 形數而言。
若不定方程(3N)^2-N+(B-1)/36=W^2 有整數解,
則 6(3N-W)+1 是小因子數;6(3N+W)-1 是大因子數。
若不定方程 (3N)^2+N+(B-1)/36=W^2 有整數解,
則 6(W-3N)-1 是小因子數;6(W+3N)+1 是大因子數。
兩式都無解,是素數。
命題 8對於B=36N+5 形數而言。
若不定方 (3N)^2+2N+(B-5)/36=W^2+W 有整數解,
則 6(W-3N)+1 是小因子數,6(W+3N+1)-1 是大因子數。
若不定方程 (3N+2)^2+4N+2+(B+31)/36=W^2+W 有整數解,
則 6(W-3N-2)-1 是小因子數,6(W+3N+3)+1 是大因子數。
兩式都無解,是素數。
命題 9對於B=36N+11 形數而言。
若不定方程 (3N+1)^2-N+(B-11)/36=W^2 有整數解,
則 6(W-3N-1)+1 是小因子數,6(W+3N+1)-1是大因子數。
若不定方程 (3N+2)^2+N+(B+25)/36=W2 有整數解,
則 6(W-3N-2)-1 是小因子數,6(W+3N+2)+1是大因子數。
兩式都無解,是素數。
命題 10 對於B=36N+17 形數而言。
若不定方程(3N+1)^2+2N+1+(B-17)/36=W^2 +W 有整數解,
則 6(W-3N-1)+1 是小因子數;6(W+3N+2)-1 是大因子數。
若不定方程 (3N+1)^2+4N+1+(B+19)/36=W^2 +W 有整數解,
則 6(W-3N-1)-1 是小因子數;6(W+3N+2)+1 是大因子數。
兩式都無解,是素數。
命題 11 對於B=36N+23 形數而言。
若不定方 (3N+2)^2-N+(B-23)/36=W^2有整數解,
則 6(W-3N-2)+1 是小因子數,6(W+3N+2)+1 是大因子數。
若不定方程 (3N+1)^2+N+(B+13)/36=W^2有整數解,
則 6(W-3N-1)-1 是小因子數,6(W+3N+1)+1 是大因子數。
兩式都無解,是素數。
命題 12 對於B=36N+31 形數而言。
若不定方程 (3N+2)^2+2N+2+(B-29)/36=W^2 +W 有整數解,
則 6(W-3N-2)+1 是小因子數,6(W+3N+3)-1是大因子數。
若不定方程 (3N)^2-4N+(B+7)/36=W^2+W有整數解,
則 6(W-3N)-1 是小因子數,6(W+3N+1)+1是大因子數。
兩式都無解,是素數。
素數定理可以給出第n個素數p(n)的漸近估計:
它也給出從整數中抽到素數的
機率 。從不大於n的自然數隨機選一個,它是素數的機率大約是1/ln n。 這定理的式子於1798年法國數學家
勒讓德 提出。1896年法國數學家
哈達瑪 (Jacques
Hadamard )和比利時
數學家 普森(Charles Jean de la Vallée-Poussin)先後獨立給出證明。證明用到了復
分析 ,尤其是黎曼函式。
對正
實數 x ,定義π(
x )為素數計數函式,亦即不大於
x 的素數個數。數學家找到了一些函式來估計π(
x )的增長。以下是第一個這樣的估計。
其中ln x為x的自然對數。上式的意思是當''x''趨近∞,π(x)與x/ln x的比值趨近1。但這不表示它們的數值隨著x增大而接近。
下面是對π(x)更好的估計:
, 其中
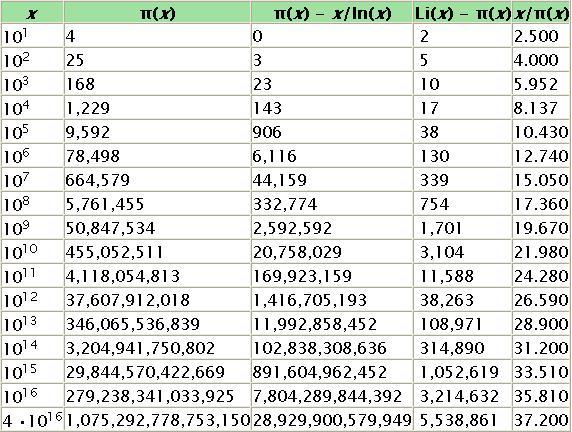
. 而關係式右邊第二項是誤差估計,詳見大O符號。 下表比較了π(
x ),
x /ln
x 和Li(
x )
素數定理 因為黎曼ζ函式與π(x)關係密切,關於
黎曼 ζ函式的
黎曼猜想 對數論很重要。一旦猜想獲證,便能大大改進素數定理誤差的估計。1901年
瑞典 數學家Helge von Koch證明出,下式與黎曼猜想等價:
素數定理有些初等證明只需用數論的方法。第一個初等證明於1949年由
匈牙利 數學家保羅·艾狄胥(“愛爾多斯”,或“愛爾多希”)和
挪威 數學家阿特利·西爾伯格合作得出。 在此之前一些數學家不相信能找出不需藉助艱深數學的初等證明。像英國數學家
哈代 便說過素數定理必須以
複分析 證明,顯出定理結果的「深度」。他認為只用到實數不足以解決某些問題,必須引進
複數 來解決。這是憑感覺說出來的,覺得一些方法比別的更高等也更厲害,而素數定理的初等證明動搖了這論調。Selberg-艾狄胥的證明正好表示,看似初等的
組合數學 ,威力也可以很大。 但是,有必要指出的是,雖然該初等證明只用到初等的辦法,其難度甚至要比用到複分析的證明遠為困難。
素數之戀 素數簡介 概念 質數又稱素數。指在一個大於1的自然數中,除了1和此
整數 自身外,不能被其他自然數整除的數。質數是與合數相對立的兩個概念,二者構成了數論當中最基礎的定義之一。基於質數定義的基礎之上而建立的問題有很多世界級的難題,如
哥德巴赫猜想 等。截至2012年6月底,質數尚未完全找到
通項公式 。
質數的無窮性的證明 質數的個數是無窮的。最經典的證明由
歐幾里得 證得,在他的《
幾何原本 》中就有記載。它使用了證明常用的方法:
反證法 。具體的證明如下:
●假設質數只有有限的n個,從小到大依次排列為p1,p2,……,pn,設 N = p1 × p2 × …… × pn,那么,N+1是素數或者不是素數。
●如果N+1為素數,則N+1要大於p1,p2,……,pn,所以它不在那些假設的素數集合中。
●如果N+1為合數,因為任何一個
合數 都可以分解為幾個素數的積;而N和N+1的最大公約數是1,所以N+1不可能被p1,p2,……,pn整除,所以該合數分解得到的素因數肯定不在假設的素數集合中。
●因此無論該數是素數還是合數,都意味著在假設的有限個素數之外還存在著其他素數。
●對任何有限個素數的集合來說,用上述的方法永遠可以得到有一個素數不在假設的素數集合中的結論。
●所以原先的假設不成立。也就是說,素數有無窮多個。
其他數學家也給出了他們自己的證明。歐拉利用
黎曼函式 證明了全部素數的倒數之和是發散的,恩斯特·庫默的證明更為簡潔,Hillel Furstenberg則用
拓撲學 加以了證明。
對於一定範圍內的素數數目的計算 儘管整個素數是無窮的,仍然有人會問“100000以下有多少個素數?”,“一個隨機的100位數多大可能是素數?”。
素數定理 可以回答此問題。
檢驗素數 檢查一個正整數N是否為素數,最簡單的方法就是試除法,將該數N用小於等於根號N的所有素數去試除,若均無法整除,N則為素數,參見素數判定法則。
2002年,印度人M. Agrawal、N. Kayal以及N. Saxena提出了AKS質數測試算法,證明了可以在多項式時間內檢驗是否為素數。
質數數表 1000以內
2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113
127 131 137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223 227 229
233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349
353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463
467 479 487 491 499 503 509 521 523 541
547 557 563 569 571 577 587 593 599 601
607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733
739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863
877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997(168個)
1000~10000
1009 1013 1019 1021 1031 1033 1039 1049 1051 1061
1063 1069 1087 1091 1093 1097 1103 1109 1117 1123
1129 1151 1153 1163 1171 1181 1187 1193 1201 1213
1217 1223 1229 1231 1237 1249 1259 1277 1279 1283
1289 1291 1297 1301 1303 1307 1319 1321 1327 1361
1367 1373 1381 1399 1409 1423 1427 1429 1433 1439
1447 1451 1453 1459 1471 1481 1483 1487 1489 1493
1499 1511 1523 1531 1543 1549 1553 1559 1567 1571
1579 1583 1597 1601 1607 1609 1613 1619 1621 1627
1637 1657 1663 1667 1669 1693 1697 1699 1709 1721
1723 1733 1741 1747 1753 1759 1777 1783 1787 1789
1801 1811 1823 1831 1847 1861 1867 1871 1873 1877
1879 1889 1901 1907 1913 1931 1933 1949 1951 1973
1979 1987 1993 1997 1999 2003 2011 2017 2027 2029
2039 2053 2063 2069 2081 2083 2087 2089 2099 2111
2113 2129 2131 2137 2141 2143 2153 2161 2179 2203
2207 2213 2221 2237 2239 2243 2251 2267 2269 2273
2281 2287 2293 2297 2309 2311 2333 2339 2341 2347
2351 2357 2371 2377 2381 2383 2389 2393 2399 2411
2417 2423 2437 2441 2447 2459 2467 2473 2477 2503
2521 2531 2539 2543 2549 2551 2557 2579 2591 2593
2609 2617 2621 2633 2647 2657 2659 2663 2671 2677
2683 2687 2689 2693 2699 2707 2711 2713 2719 2729
2731 2741 2749 2753 2767 2777 2789 2791 2797 2801
2803 2819 2833 2837 2843 2851 2857 2861 2879 2887
2897 2903 2909 2917 2927 2939 2953 2957 2963 2969
2971 2999 3001 3011 3019 3023 3037 3041 3049 3061
3067 3079 3083 3089 3109 3119 3121 3137 3163 3167
3169 3181 3187 3191 3203 3209 3217 3221 3229 3251
3253 3257 3259 3271 3299 3301 3307 3313 3319 3323
3329 3331 3343 3347 3359 3361 3371 3373 3389 3391
3407 3413 3433 3449 3457 3461 3463 3467 3469 3491
3499 3511 3517 3527 3529 3533 3539 3541 3547 3557
3559 3571 3581 3583 3593 3607 3613 3617 3623 3631
3637 3643 3659 3671 3673 3677 3691 3697 3701 3709
3719 3727 3733 3739 3761 3767 3769 3779 3793 3797
3803 3821 3823 3833 3847 3851 3853 3863 3877 3881
3889 3907 3911 3917 3919 3923 3929 3931 3943 3947
3967 3989 4001 4003 4007 4013 4019 4021 4027 4049
4051 4057 4073 4079 4091 4093 4099 4111 4127 4129
4133 4139 4153 4157 4159 4177 4201 4211 4217 4219
4229 4231 4241 4243 4253 4259 4261 4271 4273 4283
4289 4297 4327 4337 4339 4349 4357 4363 4373 4391
4397 4409 4421 4423 4441 4447 4451 4457 4463 4481
4483 4493 4507 4513 4517 4519 4523 4547 4549 4561
4567 4583 4591 4597 4603 4621 4637 4639 4643 4649
4651 4657 4663 4673 4679 4691 4703 4721 4723 4729
4733 4751 4759 4783 4787 4789 4793 4799 4801 4813
4817 4831 4861 4871 4877 4889 4903 4909 4919 4931
4933 4937 4943 4951 4957 4967 4969 4973 4987 4993
4999 5003 5009 5011 5021 5023 5039 5051 5059 5077
5081 5087 5099 5101 5107 5113 5119 5147 5153 5167
5171 5179 5189 5197 5209 5227 5231 5233 5237 5261
5273 5279 5281 5297 5303 5309 5323 5333 5347 5351
5381 5387 5393 5399 5407 5413 5417 5419 5431 5437
5441 5443 5449 5471 5477 5479 5483 5501 5503 5507
5519 5521 5527 5531 5557 5563 5569 5573 5581 5591
5623 5639 5641 5647 5651 5653 5657 5659 5669 5683
5689 5693 5701 5711 5717 5737 5741 5743 5749 5779
5783 5791 5801 5807 5813 5821 5827 5839 5843 5849
5851 5857 5861 5867 5869 5879 5881 5897 5903 5923
5927 5939 5953 5981 5987 6007 6011 6029 6037 6043
6047 6053 6067 6073 6079 6089 6091 6101 6113 6121
6131 6133 6143 6151 6163 6173 6197 6199 6203 6211
6217 6221 6229 6247 6257 6263 6269 6271 6277 6287
6299 6301 6311 6317 6323 6329 6337 6343 6353 6359
6361 6367 6373 6379 6389 6397 6421 6427 6449 6451
6469 6473 6481 6491 6521 6529 6547 6551 6553 6563
6569 6571 6577 6581 6599 6607 6619 6637 6653 6659
6661 6673 6679 6689 6691 6701 6703 6709 6719 6733
6737 6761 6763 6779 6781 6791 6793 6803 6823 6827
6829 6833 6841 6857 6863 6869 6871 6883 6899 6907
6911 6917 6947 6949 6959 6961 6967 6971 6977 6983
6991 6997 7001 7013 7019 7027 7039 7043 7057 7069
7079 7103 7109 7121 7127 7129 7151 7159 7177 7187
7193 7207 7211 7213 7219 7229 7237 7243 7247 7253
7283 7297 7307 7309 7321 7331 7333 7349 7351 7369
7393 7411 7417 7433 7451 7457 7459 7477 7481 7487
7489 7499 7507 7517 7523 7529 7537 7541 7547 7549
7559 7561 7573 7577 7583 7589 7591 7603 7607 7621
7639 7643 7649 7669 7673 7681 7687 7691 7699 7703
7717 7723 7727 7741 7753 7757 7759 7789 7793 7817
7823 7829 7841 7853 7867 7873 7877 7879 7883 7901
7907 7919 7927 7933 7937 7949 7951 7963 7993 8009
8011 8017 8039 8053 8059 8069 8081 8087 8089 8093
8101 8111 8117 8123 8147 8161 8167 8171 8179 8191
8209 8219 8221 8231 8233 8237 8243 8263 8269 8273
8287 8291 8293 8297 8311 8317 8329 8353 8363 8369
8377 8387 8389 8419 8423 8429 8431 8443 8447 8461
8467 8501 8513 8521 8527 8537 8539 8543 8563 8573
8581 8597 8599 8609 8623 8627 8629 8641 8647 8663
8669 8677 8681 8689 8693 8699 8707 8713 8719 8731
8737 8741 8747 8753 8761 8779 8783 8803 8807 8819
8821 8831 8837 8839 8849 8861 8863 8867 8887 8893
8923 8929 8933 8941 8951 8963 8969 8971 8999 9001
9007 9011 9013 9029 9041 9043 9049 9059 9067 9091
9103 9109 9127 9133 9137 9151 9157 9161 9173 9181
9187 9199 9203 9209 9221 9227 9239 9241 9257 9277
9281 9283 9293 9311 9319 9323 9337 9341 9343 9349
9371 9377 9391 9397 9403 9413 9419 9421 9431 9433
9437 9439 9461 9463 9467 9473 9479 9491 9497 9511
9521 9533 9539 9547 9551 9587 9601 9613 9619 9623
9629 9631 9643 9649 9661 9677 9679 9689 9697 9719
9721 9733 9739 9743 9749 9767 9769 9781 9787 9791
9803 9811 9817 9829 9833 9839 9851 9857 9859 9871
9883 9887 9901 9907 9923 9929 9931 9941 9949 9967
9973
10000以內共1229個
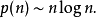
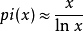
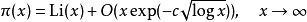

 素數定理
素數定理 素數之戀
素數之戀
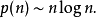
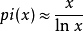
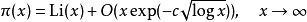

 素數定理
素數定理 素數之戀
素數之戀