定理定義 素數定理是數論中的重要定理之一。指素數分布的中心定理。
下面是對π(x)更好的估計:
, 其中
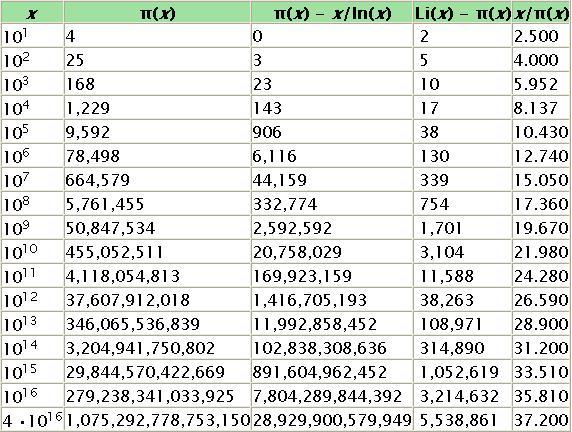
. 而關係式右邊第二項是誤差估計,詳見大O符號。 下表比較了π(x),x/ln x和Li(x): x π(x) π(x) - x/ln(x) Li(x) - π(x) x/π(x)
(如圖所示)
素數定理可以給出第n個
素數 p(n)的漸近估計:
它也給出從整數中抽到素數的
機率 。從不大於n的自然數隨機選一個,它是素數的機率大約是1/ln n。 這定理的式子於1798年法國數學家
勒讓德 提出。1896年法國數學家
哈達瑪 (Jacques
Hadamard )和比利時
數學家 普森(Charles Jean de la Vallée-Poussin)先後獨立給出
證明 。證明用到了複分析,尤其是黎曼ζ函式。 因為黎曼ζ函式與π(x)關係密切,關於
黎曼 ζ函式的
黎曼猜想 對數論很重要。一旦猜想獲證,便能大大改進素數定理
誤差 的估計。1901年
瑞典 數學家Helge von Koch證明出,下式與
黎曼猜想 等價:
素數定理 發展歷史 大約在1792年,15歲的德國天才少年
高斯 (C.Gauss)經過深入分析和例證,猜想素數在自然數中的分布密度應該是(他提出的是積分形式)。差不多在同一時候,法國數學家勒讓德(A.M.Legendre)通過數值計算,於1808年提出這樣一個經驗公式: 當x→+∞時,π(x)趨向於,這裡的π(x)即不大於正實數x的素數個數。容易看到,高斯和勒讓德提出的漸進公式是等階的,實際上都等同於猜想π(x)~(不過高斯更深刻和精確)。這就是19世紀最著名的數學難題——素數定理。這個猜想是非常令人驚異的,因為素數在自然數中的分布可以說相當“雜亂無章”,但它竟然還能用這樣簡單的公式來描述!
首先對素數定理的研究作出重要貢獻的是俄國大數學家
切比雪夫 (P. Chebyshev),他證明: 存在兩個正常數C
1 和C
2 ,使不等式≤π(x)≤對充分大的x成立,並且相當精確地定出了C
1 和C
2 的數值。他還證明,如果的極限存在,則必定是1。這些無疑都是很重要的進展,但遺憾的是,用切比雪夫的方法無法證明最後的結果。
1896年,兩位年輕的數學家
阿達馬 (J.Hadamard)和德·拉·瓦萊布桑(C. J. de la Vallée Poussin)按照大數學家、高斯的學生黎曼(B. Riemann)的思路,終於各自獨立地利用高深的整函式理論證明了素數定理,從而解決了這個有著一個世紀歷史的難題。
1949年,兩位年輕的數學家——31歲的賽爾伯格(A. Selberg)和35歲的愛多士(P. Erdös)分別獨立地證明了素數定理。與以往證明不同的是,他們沒有用到ζ函式,而且除了極限、e和logx的簡單性質外,沒有用到任何高等數學知識,甚至連微積分都沒用到!可以說,他們給出的是一個完全“初等”的證明,這一結果轟動了整個數學界後來有人用1+x++…+代替e,用1++…+代替logx (n≤x),給出了一個連指數、對數函式都不需要的初等證明。賽爾伯格由於這項成就及其他工作而獲得了菲爾茲獎,愛多士則與陳省身一起獲得了
沃爾夫數學獎 。
初等證明 素數定理有些初等證明只需用數論的方法。第一個初等證明由1949年由
匈牙利 數學家保羅·
厄多斯 (另譯埃爾德什、艾狄胥、“愛爾多斯”,或“愛爾多希”)和
挪威 數學家阿特利·西爾伯格合作得出。 在此之前
一些數學家不相信能找出不需藉助艱深數學的初等證明。像英國數學家
哈代 便說過素數定理必須以
複分析 證明,顯出定理結果的「深度」。他認為只用到實數不足以解決某些問題,必須引進
複數 來解決。這是憑感覺說出來的,覺得一些方法比別的更高等也更厲害,而素數定理的初等證明動搖了這論調。Selberg-艾狄胥的證明正好表示,看似初等的
組合數學 ,威力也可以很大。 但是,有必要指出的是,雖然該初等證明只用到初等的辦法,其難度甚至要比用到複分析的證明遠為困難。
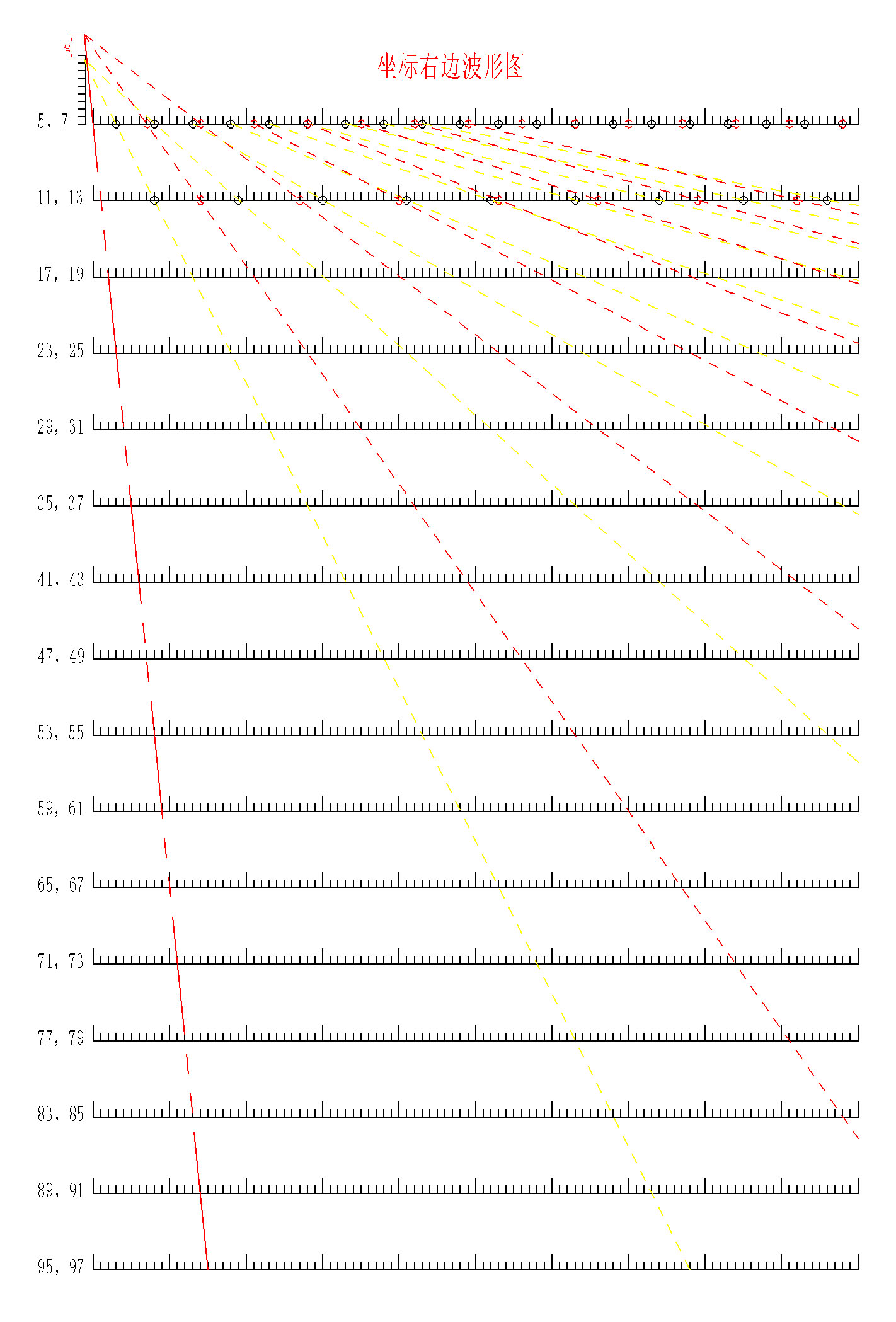
素數之戀 驗證推導 除2、3之外,所有6n±1都可置於一條坐標上,將6n+1分布在左邊,那么中心點為1,右側為6n-1。反正則中心點為-1。坐標上的每個數字產生一條波形,未被覆蓋的點就是素數。波長等於數字自身。
將每條波形拆分,坐標左邊和坐標右邊形成兩條波形,存在兩個焦點,附圖:
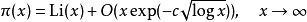

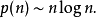

 素數定理
素數定理 素數之戀
素數之戀