基本介紹
- 中文名：素數無限定理
- 套用學科：數學
- 適用領域範圍：證明題
- 用於：歐幾里得的證明
術語定義,主要貢獻,
術語定義
數學家把自然數按照乘法性質分為三類：
一，自然數“1”。
二，素數，就是沒有比自身小的素數可以整除，例如2,3,5，....
三，複合數，至少有兩個素因數，例如：4,6,8,9,10,12,15，....
素數是無限的還是有限的？兩千年前的古希臘數學家歐幾里得證明了這個問題，被認為是經典之作。以後又出現十幾種證明方法。例如歐拉的證明。
主要貢獻
歐幾里得的證明
證明:
假設素數只有有限個，按照大小順序，.分別記為：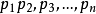
.。最大的素數
.。
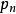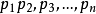
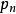
設所有乘積加1為：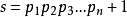
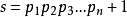
現在考慮s是什麼？
如果s是素數，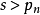
，與假設矛盾。
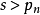
如果s是合數，s不能被已知素數整除。得出矛盾，說明原來假設素數是有限的是錯誤的。證畢。
【初等數論】（u杜德利著，科學出版社）
,一般證明
證明：
假設素數有限，按照大小順序，分別記為：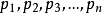
。
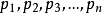
現在設：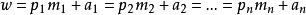
。其中，
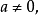
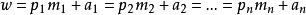
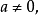
w與所有素數互素。
現在問：
是素數還是合數？
如果w是素數，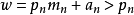
。與假設矛盾。
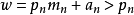
如果是合數，不存在與所有素數互素的合數（因為複合數至少有兩個素因數）。
【素數個數問題三種新證法】（中等數學）
