整數分拆理論,主要是研究各種類型的分拆函式的性質及其相互關係。早在中世紀,就有關於特殊的整數分拆問題的研究。18世紀40年代,L.歐拉提出了用母函式法(或稱形式冪級數法)研究整數分拆,證明了不少有重要意義的定理,為整數分拆奠定了理論基礎。解析數論中的圓法的引進,使整數分拆理論得到了進一步發展。整數分拆與模函式有密切關係,並在組合數學、群論、機率論、數理統計學及質點物理學等方面都有重要套用。
基本介紹
- 中文名:整數分拆
- 外文名:Integer splitting、Partition
- 科目:數學
- 套用:研究各種分拆函式性質及相互關係
- 提出者:萊昂哈德·歐拉(Leonhard Euler)
- 相關人物:G.H.哈代,斯里尼瓦瑟·拉馬努金
原理
分類

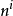


例子
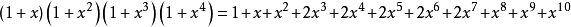


拆分數估計


拆分數估計定理證明




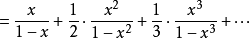












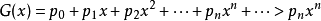









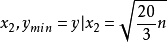

拆分數性質
性質一
性質二
性質三
拆分數計算方法
遞推法



#include <stdio.h>#define MYDATA long longconst MYDATA MOD = 1000000007;#define MAXNUM 100005 //最高次數 //遞歸法求解整數劃分unsigned long GetPartitionCount(int n, int max){ if (n == 1 || max == 1)return 1; if (n < max)return (GetPartitionCount(n, n)) % MOD; if (n == max)return (1 + GetPartitionCount(n, n - 1)) % MOD; else return (GetPartitionCount(n - max, max) + GetPartitionCount(n, max - 1)) % MOD;}int main(int argc, char **argv){ int n; int m; unsigned long count; while (1) { scanf("%d", &n); if (n <= 0) return 0; m = n; count = GetPartitionCount(n, m); printf("%d\n", count); } return 0;}動態規劃法
#include <iostream>#define MYDATA long longconst MYDATA MOD = 1000000007;#define MAXNUM 1005 //最高次數 unsigned long ww[MAXNUM * 11][MAXNUM * 11];unsigned long dynamic_GetPartitionCount(int n, int max);using namespace std;int main(int argc, char **argv){ int n; int m; unsigned long count; while (1) { cin >> n; cout << dynamic_GetPartitionCount(n, n) << endl; } return 0;}unsigned long dynamic_GetPartitionCount(int n, int max){ for (int i = 1; i <= n; i++) for (int j = 1; j <= i; j++) { if (j == 1 || i == 1) { ww[i][j] = 1; } else { if (j == i) ww[i][j] = (ww[i][j - 1] + 1) % MOD; else if ((i - j) < j) ww[i][j] = (ww[i - j][i - j] + ww[i][j - 1]) % MOD; else ww[i][j] = (ww[i - j][j] + ww[i][j - 1]) % MOD; } } return ww[n][max];}生成函式法


































#include <iostream>#include <string.h>#include <stdio.h>using namespace std;#define MYDATA long longconst MYDATA MOD = 1000000007;const int N = 100005;int c1[N], c2[N];int main(int argc, char** argv){ int n, i, j, k; while (cin >> n) { if (n == 0) break; for (i = 0; i <= n; i++) { c1[i] = 1; c2[i] = 0; } for (i = 2; i <= n; i++) { for (j = 0; j <= n; j++) for (k = 0; k + j <= n; k += i) c2[k + j] = (c2[k + j] + c1[j]) % MOD; for (j = 0; j <= n; j++) { c1[j] = c2[j]; c2[j] = 0; } } cout << c1[n] << endl; } return 0;}五邊形數法









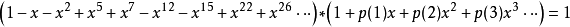



#include <iostream>using namespace std;#define MYDATA long longconst MYDATA MOD = 1000000007;#define AMS 100005MYDATA pp[AMS];MYDATA asist[2 * AMS];void myinit(){ for (int i = 0; i < AMS; i++) { /*算出五角數(正常五角數為1,5,12,22.... k*(3*k-1)/2)*/ /*此部分,需要算出的是分割函式(1,2,5,7,12,15,22,26..... [k*(3*k-1)/2,k*(3*k+1)/2 ])*/ asist[2 * i] = i * (i * 3 - 1) / 2; asist[2 * i + 1] = i * (i * 3 + 1) / 2; }}void mymethod(){ pp[1] = 1; pp[2] = 2; pp[0] = 1; for (int i = 3; i < AMS; i++) { int k = 0; int flags; pp[i] = 0; /*pp[n]=pp[n-1]+pp[n-2]-pp[n-5]-pp[n-7]+pp[12]+pp[15] -.... ..... [+pp[n-k*[3k-1]/2] + pp[n-k*[3k+1]/2]]*/ for (int j = 2; asist[j] <= i; j++) { /*說明:式子中+MOD是必須的,否則輸出可能出錯(有可能為負數)*/ flags = k & 2; if (!flags) pp[i] = (pp[i] + pp[i - asist[j]] + MOD) % MOD; else pp[i] = (pp[i] - pp[i - asist[j]] + MOD) % MOD; k++; k %= 8; } }}int main(int argc, char** argv){ int n; myinit(); mymethod(); while (1) { cin >> n; cout << pp[n] << endl; } return 0;}
