整數集劃分問題就是將一個整數集S={1,2,…,n}劃分成r個子集(或類)的有關性質與數量估算的著名難題。所謂將集合S劃分為r個子集就是S=S1∪S2∪...∪Sr,其中Si∩Sj=∅(i≠j,i,=1,2,…,r)。
基本介紹
- 中文名:整數集劃分問題
- 外文名:partition problems for integer set
- 所屬學科:數學
- 相關問題:集合的劃分
- 相關方法:構造法、反證法、數學歸納法等
基本介紹,相關研究,范·德·瓦爾登數問題,舒爾問題,拉多問題,集合的劃分,例題詳解,
基本介紹
整數集劃分問題就是將一個整數集S={1,2,…,n}劃分成r個子集(或類)的有關性質與數量估算的著名難題。所謂將集合S劃分為r個子集就是

相關研究
范·德·瓦爾登數問題
1927年,荷蘭數學家范·德·瓦爾登(Van der Waerden,B.L.)證明了一個著名的定理:對於任給的正整數r和k,必存在一個正整數n=n(r,k),將整數集S={1,2,…,n}劃分成r個子集,則至少有一個子集含有k+1項的等差數列(也稱算術數列),對於給定的r與k,n(r,k)的最小值記為W(r,k),稱為范·德·瓦爾登數。
更一般的范·德·瓦爾登定理:對於給定的正整數r和k1,k2,…,kr,必存在正整數n=n(r;k1,k2,…,kr),將整數集S={1,2,…,n}劃分成r個子集,使得在每個子集Si(i=1,2,…,r)中含有ki+1項等差數列,這樣的最小的n值記為W(r;k1,k2,…,kr),也稱為范·德·瓦爾登數。計算范·德·瓦爾登數或估計其界限是一項重要課題。
1970年,瓦泰爾(Chvatal,V.)計算出:W(2;2,2)=9,W(2;2,3)=18,W(2;2,4)=22,W(2;2,5)=32,W(2;2,6)=46。
1979年,比利(Beeler,M.D.)和奧尼爾(O'Neil,P.E.)計算出:W(2;2,7)=58,W(2;2,8)=77,W(2;2,9)=97。
此外,還有
此外,還有
W(2;3,3)=35,W(2;3,4)=55(瓦泰爾)。
W(2;3,5)=73(比利和奧尼爾)。
W(2;4,4)=178(斯蒂文斯(Stevens,R.S.)和香塔厄姆(Shantaram,R.))。
W(3;2,2,2)=27(瓦泰爾)。
W(3;2,2,3)=51(布朗(Brown,T.C.))。
W(4;2,2,2,2)=76(比利和奧尼爾)。
匈牙利數學家愛爾特希(Erdos,P.)與拉多(Radó,R.)證明了W(r,k)>(2krk)1/2。此後,莫澤(Moser,L.)、施密特(Schmidt,W.M.)、伯利肯姆波(Berlekamp,E.R.)將上述結果相繼改進成
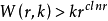



舒爾問題
猶太人數學家舒爾(Schur,I.)曾證明了一個著名定理:對於給定的正整數r,以任意方式將整數集S={1,2,…,[r!e]}劃分成r個子集,則必有某一個子集的數使方程x+y=z有解,式中[x]表示不大於x的最大整數。1973年,歐文(Irving,R.W.)將舒爾的上界減少到

對於給定的正整數r,將滿足下列條件的最大整數記為n=n(r):存在對整數集S={1,2,…,n(r)}的一個劃分,使得在任一個子集Si(i=1,2,…,r)中都沒有x+y=z的解,將這種劃分所得的子集稱為無和子集(sumfree subset)。1961年,鮑默特(Baumert,L.D.)計算出n(4)=44。例如將S={1,2,…,44}可劃分成下列4個無和子集:
{1,3,5,15,17,19,26,28,40,42,44};
{2,7,8,18,21,24,27,33,37,38,43};
{4,6,13,20,22,23,25,30,32,39,41};
{9,10,11,12,14,16,29,31,34,35,36}.
1975年,弗雷德里克森(Fredricksen,H.)證明了n(5)≥157,對於n(r)的下界估計有(舒爾證得)

拉多問題
數學家拉多(Radó,R.)研究了一些廣義范·德·瓦爾登問題與廣義舒爾問題。他證明了,對任何正整數a,b,c,一定存在一個整數n,無論怎樣將S={1,2,…,n}劃分成兩個子集,至少在一個子集中使方程ax+by=cz有解。他給出了一個確定n值的方法,但不是最好的。例如,對於方程2x+y=5z,拉多定理給出的n=20,實際上只要n=15就夠了,即不論如何將S={1,2,…,15}劃分成兩個子集,必在一個子集中使方程2x+y=5z有解(x,y,z)。
設r是給定的正整數,如果存在一個最小的整數n(r),無論怎樣劃分S={1,2,…,n(r)}成r個子集,總存在一個子集含有方程a1x1+a2x2+…=0的解,其中ai(i=1,2,…)是非零整數,則稱此方程是r葉正則(r-fold regular),簡稱r正則,上述的拉多定理表明,方程ax+by=cz是2葉正則的。
自然數都可表示成5·β形式,其中α=0,1,2,…而5不能整除整數β,則按α取偶數或奇數,β≡±1或±2(mod 5),可將自然數集分成4個子集:
{5αβ|α是偶數,β≡±1(mod 5)};
{5αβ|α是偶數,β≡±2(mod 5)};
{5αβ|α是奇數,β≡±1(mod 5)};
{5αβ|α是奇數,β≡±2(mod 5)}.
可以證明,方程2x+y=5z,在上述任一子集中都無解,因而,此方程不是4葉正則的。拉多提出了一個至今尚未解決的問題:對於每一個正整數r,是否存在這樣的方程,它是r葉正則的,但不是(r+1)葉正則的?
集合的劃分
1. ∀m(m∈M→Am⊆A∧Am≠∅);
2. ∀m∀n(m∈M∧n∈M∧m≠n→Am∩An=∅);
3.  ,
,

則稱集族A是集合A的一個劃分。集A的劃分A={Am}m∈M可以確定A上的一個等價關係R,只要定義:a,b屬於同一個Am時,aRb;a,b屬於不同的Am時, 。反之,如果R是A上的等價關係,對a∈A,作集合[a]R,使得b∈[a]R
。反之,如果R是A上的等價關係,對a∈A,作集合[a]R,使得b∈[a]R (b∈A∧aRb),則由所有不同的[a]R組成的集合是A的一個劃分,即為A關於A上的等價關係R的商集A/R,劃分是一個有用的概念,例如,可將人類按性別劃分成男人和女人,也可以按年齡來劃分、按職業來劃分等。
(b∈A∧aRb),則由所有不同的[a]R組成的集合是A的一個劃分,即為A關於A上的等價關係R的商集A/R,劃分是一個有用的概念,例如,可將人類按性別劃分成男人和女人,也可以按年齡來劃分、按職業來劃分等。


例題詳解
將一個給定的集合P分拆成若干個非空真子集 ,使得
,使得



集合的劃分問題特別是整數集及其子集的劃分問題是國內外較高層次的數學競賽中的熱門試題之一。這方面的問題常見的有兩類:存在型和不存在型。從解決這些問題的方法來看,常用的有:構造法、反證法、數學歸納法、局部調整法、無窮下降法和從特殊情況入手等。從涉及的知識來看,要用到整數的基本性質,邏輯中的矛盾律和排中律等。
集合的劃分,實質上是對集合進行一個分類,到底如何分?我們說,具體問題具體對待。
【例1】設n≥15是自然數,A、B都是{1,2,…,n}的真子集, 且{1,2,…,n}=AUB。
且{1,2,…,n}=AUB。

證明:A或者B中必有兩個不同數的和為完全平方數。
分析: 由此題的結論可以看出,要證明的是A、B中至少有一個集具有性質:在該集中存在兩個不同數的和為完全平方數。因為是“至少”與“存在”的問題,所以可以考慮用反證法。
證明: 假設結論不成立,則存在{1,2,…,n}的兩個真子集, 且{1,2,…,n}=AUB,使得無論是A還是B中的任何兩個不同的數的和都不是完全平方數。
且{1,2,…,n}=AUB,使得無論是A還是B中的任何兩個不同的數的和都不是完全平方數。

不失一般性,不妨設1∈A,則 ,否則1+3=22,與反證法的假設矛盾,從而3∈B,同樣
,否則1+3=22,與反證法的假設矛盾,從而3∈B,同樣 所以,6∈A,這樣
所以,6∈A,這樣 即10∈B.因n≥15,故15或者在A中,或者在B中.但當15∈A時,閒1 ∈A,1+15=42,矛盾;當15∈B時,因10∈B,10+15=52,仍然矛盾。因此,反證法法的假設是錯的,故原結論成立。
即10∈B.因n≥15,故15或者在A中,或者在B中.但當15∈A時,閒1 ∈A,1+15=42,矛盾;當15∈B時,因10∈B,10+15=52,仍然矛盾。因此,反證法法的假設是錯的,故原結論成立。



【例2】 求出有下列性質的所有正整數n:集合{n,n+1,n+2,n+3,n+4,n+5}可以劃分為兩個無公共元素的非空子集,使得一個子集中所有元素的積和另一子集的所有元素之積相等。(第12屆IMO試題)
解: 設n為具有上述性質的數,根據分解唯一性定理,n,n+1,n+2,n+3,n+4,n+5中任一個數的質因數,必定還是另一個數的因數,設d是n+k(k=0,1,…,5)的一個質因數,則d也是n+j(j≠k)的質因數,於是d|(n+k)-(n+j),即 因
因 故d只能為2,3,5。並且n+1,n+2,n+3,n+4這四個數的質因數只能有2和3,但這四個數中,有兩個是奇數,這兩個數不能含有因數2,只能都是3的乘冪,但這是不可能的。因為,當h>1,m>1時,
故d只能為2,3,5。並且n+1,n+2,n+3,n+4這四個數的質因數只能有2和3,但這四個數中,有兩個是奇數,這兩個數不能含有因數2,只能都是3的乘冪,但這是不可能的。因為,當h>1,m>1時, 不可能等於2,所以適合於題設的n不存在。
不可能等於2,所以適合於題設的n不存在。



說明:因題目的結論要求求出具有題設條件的所有正整數n,因此,我們自然想到n就具有這樣的性質。進一步探討n的結構特點,可是經過幾步推理之後,n根本就不存在,從而問題得到解決。
【例3】 設r是任意一個自然數,若將全體自然數所成的
集N分拆成r個兩兩不相交的子集 ,則在這些子集中必存在某個子集A,具有性質(*):存在m∈N,使得對任何正整數k,都能找到
,則在這些子集中必存在某個子集A,具有性質(*):存在m∈N,使得對任何正整數k,都能找到 ,滿足
,滿足 。(第31屆IMO預選題)
。(第31屆IMO預選題)



證明: 為了證明本命題,我們從特殊情況入手,考慮N的一種特殊的子集,若N的子集P包含有任意有限長度的相繼自然數段,則稱P為N的“長子集”.我們將證明一個加強的命題(I):若將N的長子集P分拆成r個兩兩不相交的子集 ,則這些子集中必存在某個子集A具有性質(*)。
,則這些子集中必存在某個子集A具有性質(*)。

先用數學歸納法證明命題(I).當r=1時,命題(I)顯然成立,設r=n時,命題(I)成立,考察r=n+1時的情形。
設長子集P拆成n+1個兩兩不相交的子集 ,記
,記 ,若Q是N的長子集,則由歸納假設知,命題(I)已經成立,若Q不是長子集,則存在某正整數m1,使得Q不包含任何相繼的m1個自然數,由於P是N的長子集,因而對於任意給定的k,集P必定含有長為km1的連續自然數段,將這個自然數段分成k小段
,若Q是N的長子集,則由歸納假設知,命題(I)已經成立,若Q不是長子集,則存在某正整數m1,使得Q不包含任何相繼的m1個自然數,由於P是N的長子集,因而對於任意給定的k,集P必定含有長為km1的連續自然數段,將這個自然數段分成k小段 每小段恰有相繼的m1個自然數,由於Q不包含長為k的相繼自然數段,因此對於每個Pi(1≤i≤k)都至少存在一個
每小段恰有相繼的m1個自然數,由於Q不包含長為k的相繼自然數段,因此對於每個Pi(1≤i≤k)都至少存在一個 ,但
,但 ,因
,因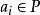 ,故必有
,故必有 ,這樣,我們已有
,這樣,我們已有 。顯然這樣確定的
。顯然這樣確定的 必滿足
必滿足 ,這就證明了當r=n+1時,命題(I)也成立,由數學歸納法即知,命題(I)對任何自然數r成立。
,這就證明了當r=n+1時,命題(I)也成立,由數學歸納法即知,命題(I)對任何自然數r成立。





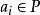




由於N也是它自身的長子集,於是由加強的命題(I)即知原命題成立。
更多例題及其證明方法請參考文後參考書籍。

