指把一個正整數n寫成多個大於等於1且小於等於其本身的整數的和，則其中各加數所構成的集合為n的一個劃分。這是一個典型的遞歸算法。
基本介紹
- 中文名：整數劃分
概念,求劃分個數,分析,JAVA實現,利用計算機計算（C語言）,求具體劃分集合,分析,利用計算機求解（C語言）,
概念
所謂整數劃分，是指把一個正整數n寫成為
其中，
為正整數，並且
；
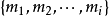為n的一個劃分。
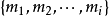
如果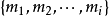 中的最大值不超過m，即
，則稱它屬於n的一個m劃分。
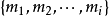
求劃分個數
分析
這裡我們記n的m劃分的個數為
。
例如，當n=4時，有5個劃分，即
，
，
，
，
。
注意：
和
被認為是同一個劃分。
根據n和m的關係，考慮一下幾種情況：
（一）當
時，無論m的值為多少
，只有一種劃分，即
。
（二）當
時，無論n的值為多少，只有一種劃分，即n個1，
。
（三）當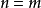
時，根據劃分中是否包含n，可以分為以下兩種情況：
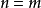
（1）劃分中包含n的情況，只有一個，即
。
（2）劃分中不包含n的情況，這時劃分中最大的數字也一定比n小，即n的所有
劃分。
因此
。
（四）當
時，由於劃分中不可能出現負數，因此就相當於
。
（五）當
時，根據劃分中是否包含最大值m，可以分為以下兩種情況：
（1）劃分中包含m的情況，即
，其中
的和為n-m，因此這種情況下為
。
（2）劃分中不包含m的情況，則劃分中所有值都比m小，即n的
劃分，個數為
。
因此
。
綜上所述：
JAVA實現
/函式：q(int n,int m)//作用：用來得到正整數n，最大加數不大於m的劃分個數public static int q(int n,int m){ //若正整數或最大加數小於1，則返回0 if(n<1||m<1) return 0; //若正整數或最大加數等於1，則劃分個數為1（n個1相加） if(n==1||m==1) return 1; //若最大加數實際上不能大於正整數n，若大於則劃分個數等於最大加數為n的劃分個數 if(n<m) return q(n,n); //若正整數等於最大加數，則劃分個數等於 if (n==m) return 1+q(n,n-1); return q(n,m-1)+q(n-m,m);} 利用計算機計算（C語言）
#include<stdio.h>void main(){ int equation(int n,int m); int n,m; printf("Please input 'n'(0<n<100):"); scanf("%d",&n); printf("Please input 'm'(0<m<=n):"); scanf("%d",&m); printf("quantity:%d\n",equation(n,m));}int equation(int n,int m){ if(n==1||m==1) return (1); else if(n<m) return equation(n,n); else if(n==m) return 1+equation(n,n-1); else return equation(n-m,m)+equation(n,m-1);}求具體劃分集合
分析
把一個正整數n分成
，若使
，可求出一種劃分，再使x遞減，令x是劃分好的數，按此方法繼續對y繼續進行分解，以此類推，直到
（不包含 ）為止，這樣就求出了所有劃分。
在分解時應保證分解數x有序，即上一次的x要大於等於這一次的x，以避免求出元素相同但位置不同的結果。
例：當
時，部分過程如下圖所示：
當n=6時的部分過程利用計算機求解（C語言）
#include<stdio.h>int x[50]={0};void main(){ void split(int n,int k); int n; printf("Please input 'n'(0<n<100):"); scanf("%d",&n); split(n,0);}void split(int n,int k)//k是數組中的位置，亦是遞歸層數{ void display(int k); int i; if(n==0)//分解完成，輸出結果 display(k); else for(i=n;i>0;i--) if(k==0||i<=x[k-1]) { x[k]=i;//寫入數組 split(n-i,k+1); }}//輸出數組前k項void display(int k){ int i; for(i=0;i<k;i++) printf("%d ",x[i]); printf("\n");}