拆分數估計

整數的拆分問題，即將正整數n分解為若干個正整數的和。不考慮起求和的順序。正整數的一種拆分可以理解為將n個無區別的球，放入n個無區別的盒子，其每種方案就是一種拆分。一般來說現在整數的拆分問題求解的常用工具是母函式和Ferrers圖像。整數拆分在組合數學、群論、機率論、數理統計學等方面都有重要套用，但當n比較大時，計算機複雜度高，所以這裡給出一種關於拆分數估計的定理與證明，便於拆分數的推廣與套用。

基本介紹

• 中文名：拆分數估計
• 外文名：Integer splitting estimation
• 套用學科：數學
• 適用領域範圍：組合論，圖論

拆分數估計定理

正整數n拆分成若干個正整數之和，其不同的拆分數用p(n)表示，{p(n)}的母函式為：

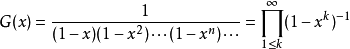
則拆分數估計可以表示為：

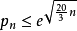
證明

令

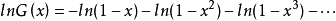
根據馬克羅林級數：

所以：

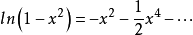
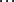
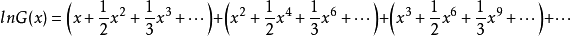
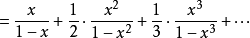
而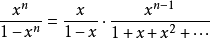

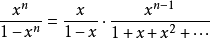
又由於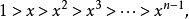

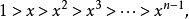
所以有下式成立：

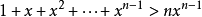
因此有

所以

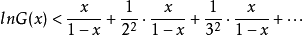
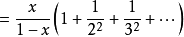
但是

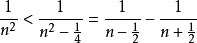
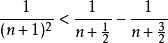
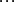
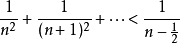
所以

設 有

曲線y=lnx是向上凸的，所以曲線y=lnx在（1，0）的切線為y=x-1,即有 .

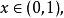
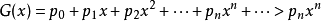
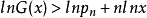
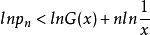
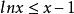
所以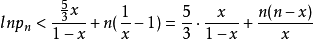

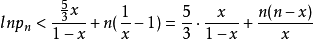
對於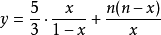 ，令其一階導 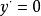，方程的解為

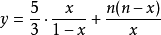
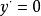
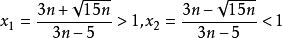
又因為y的二階導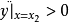 ,所以y的極小值為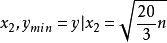

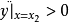
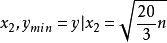
所以

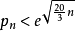
套用

1.一般情況下，p(n)的遞推關係比較複雜，但很多情況我們往往不需要知道確切的拆分數，我們可以用拆分數估計定理來估計拆分數的上界；p(n)的漸進公式也是很多學者研究的課題。

2. 圖論，組合論等領域中有廣泛套用。