基本介紹
定義

五邊形數測試

表示整數
廣義五邊形數


求拆分數



 圖1.五邊形數
圖1.五邊形數





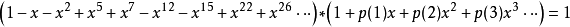


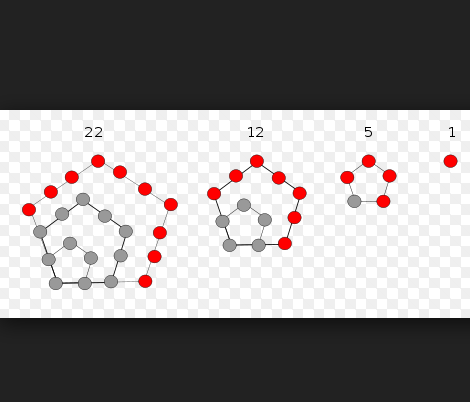







 圖1.五邊形數
圖1.五邊形數





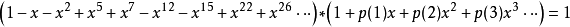


五邊形數是能排成五邊形的多邊形數。其概念類似三角形數及平方數,不過五邊形數和三角形數及平方數不同,所對應的形狀沒有旋轉對稱(Rotational symmetry)的特性。...
五邊形數定理是一個由歐拉發現的數學定理,描述歐拉函式展開式的特性。...... 五邊形數定理是一個由歐拉發現的數學定理,描述歐拉函式展開式的特性。 [1] ...
有些數既可排成三角形,又可排成正方形,例如36(這些數稱為三角平方數):...五邊形數:1:+ x5:x x+ + x x+ + x x12:x xx x x x...
前15項的中心五邊形數為1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526...(OEIS中的數列A005891).有形...
古希臘的畢達哥拉斯學派認為數是萬物的本原,因此極為重視數的理論研究,他們常...每個圖形的點數分別稱為三角形數、四邊形數、五邊形數……除三角形數外,其餘的...
中心五邊形數 1,6,16,31,51 中心多邊形數是一種有形數的級數,它由中間的一點開始,以後每層就以固定的邊數包圍在其四周。層的每邊都比上一層多一點,,即是...
設五邊形數的生成函式為,那么有:以上是五邊形數的情況。下面是關於五邊形數定理的內容:五邊形數定理是一個由歐拉發現的數學定理,描述歐拉函式展開式的特性。歐拉函式...
16(十六),是15與17之間的自然數。16是4的平方。...... 第3箇中心五邊形數。 和15組成了一對魯斯·阿倫數對。 十六進制常用於電腦系統中。 四四十六,二八十...
117(一百一十七)是116和118之間的一個自然數,是一個奇數、合數,也是一個...五邊形數 40邊形數 它是6²與9²的和 117在其它領域中 編輯 中華...
