費馬多邊形數定理是一個定律,定義為每一個正整數都可以表示為最多n個n邊形數的和。也就是說,每一個正整數一定可以表示為不超過三個的三角形數之和、不超過四個的平方數之和、不超過五個的五邊形數之和,依此類推。
基本介紹
- 中文名:費馬多邊形數定理
- 外文名:Fermat polygonal number theorem
- 提出者:費馬
- 套用學科:數學
- 適用領域範圍:幾何學
- 適用領域範圍:幾何學
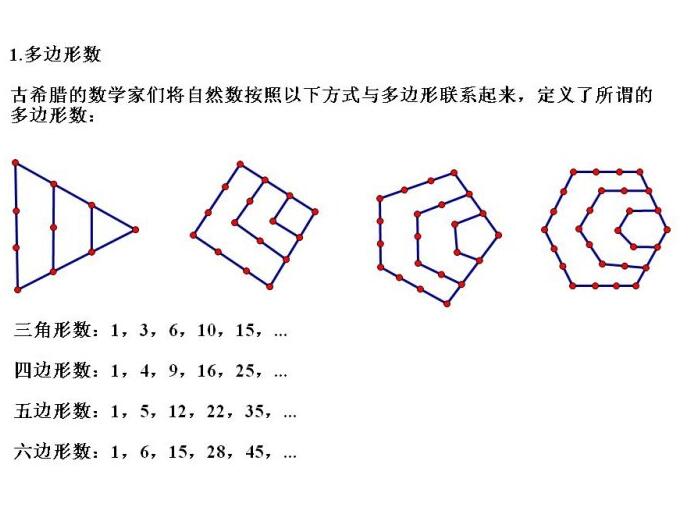
費馬多邊形數定理是一個定律,定義為每一個正整數都可以表示為最多n個n邊形數的和。也就是說,每一個正整數一定可以表示為不超過三個的三角形數之和、不超過四個的平方數之和、不超過五個的五邊形數之和,依此類推。
費馬多邊形數定理是一個定律,定義為每一個正整數都可以表示為最多n個n邊形數的和。也就是說,每一個正整數一定可以表示為不超過三個的三角形數之和、不超過四...
1是任何多邊形數的第一項。第n個s邊形數的公式是 \frac{n((s-2)n-(s-4))}{2}費馬多邊形數定理指出每個數最多是n個n邊形的和。...
若n是自然數,則x是五邊形數,而且恰為第n個五邊形數。若n不是自然數,則x不是五邊形數。五邊形數表示整數 編輯 依照費馬多邊形數定理,任何整數都可以表示為不超過...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...凡·奧貝爾定理芬斯勒-哈德維格爾定理反函式定理費馬多邊形數定理G...
四平方和定理說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。...
它是費馬多邊形數定理和華林問題的特例。注意有些整數不可表示為3個整數的平方和,例如7。2.歷史1. 1743年,瑞士數學家歐拉發現了一個著名的恆等式: 。根據上述...
四平方和定理說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。...
在數論中,歐拉定理(Euler Theorem,也稱費馬-歐拉定理或歐拉函式定理)是一個關於...▪ 分式 ▪ 複數 ▪ 三角形 ▪ 多面體 ▪ 多邊形 歐拉...
二百五十七邊形是多邊形的一種。共有257條邊,257個頂點,內角和45900°,對角...在高斯得出此定理之前,已知的費馬數只有3、5、17、257、65537。...
他與他的學派致力於一些特殊整數(如親和數、完全數、多邊形數)及特殊不定方程...例如“初等數論”,由公理(例如等量公理),定理(例如費馬小定理),原理(例如抽屜...
001 算術基本定理002 戶國剩餘問題003 牛吃草問題004 費馬數005 梅森數...023 多邊形數024 巴赫猜想025 生素數猜想026 圓內整點問題027 卡塔蘭猜想...
1 介紹 2 性質 3 與正多邊形的聯繫 4 與費馬最後定理的聯繫 5 參見 分圓域介紹 編輯 在數論中,分圓域是在有理數域Q中添加複數單位根進行擴張而得到的...
