基本介紹
發展簡史
驗證推導










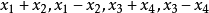
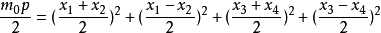


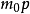






















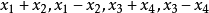
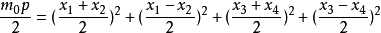


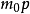












四平方和定理說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。...
四平方數和定理(theorem on the sum of foursquares)亦稱拉格朗日四平方數和定理。四平方數和問題是著名的數論問題.由拉格朗日(La-grange, J.-L.)最終解決,...
四平方和定理說明每個正整數均可表示為4個整數的平方和。它是費馬多邊形數定理和華林問題的特例。...
拉格朗日定理存在於多個學科領域中,分別為:微積分中的拉格朗日中值定理;數論中的四平方和定理;群論中的拉格朗日定理 (群論)。...
一個平方數是兩個相鄰三角形數之和。兩個相鄰平方數之和為一個中心正方形數。所有的奇數平方數同時也是中心八邊形數。 四平方和定理說明所有正整數均可表示為最...
布魯克-賴瑟-喬拉定理(Bruck-Ryser-Chowla theorem)是反映對稱設計存在的必要條件的一個事實,若(v,k,λ)-SBIBD存在,記n=k-λ,則當v為偶數時,n為平方數;當...
第一章 整數平方和——能表示嗎?1.1 二平方和——高斯定理1.2 四平方和——兼談域和四元數體1.3 二元二次型1.4 三平方和...
華林自己推測g(2)=4,g(3)=9,g(4)=19。1770年,拉格朗日證明了四平方和定理,指出g(2)=4。1909年亞瑟·韋伊費列治證明了g(3)=9。...
4,數字,(發音:中文sì,讀第四聲。英文four),是3與5之間的自然數,也是正整數、偶數、有理數、實數。4是正整數中最小的合數,是數字2的2倍。它也是一個平方...
1.2 二平方和定理與四平方和定理習題第2章 凸體的多邊形逼近2.1 Dowker定理2.2 橢圓的一個極值性質2.3 凸體的多胞形逼近習題...
19.14 定理362和定理363的證明 29419.15 Ramanujan連分數 296本章附註 297第20 章用兩個或四個平方和表示數 30020.1 Waring問題:數g(k)和G(k) 300...
