基本介紹
形數亦稱擬形數、垛積數,是一種與圖形有關的數,古希臘
畢達哥拉斯學派在研究
數論時非常注意形與數的關係,形數便是數與形相結合的一種概念,他們用點子排成三角形、正方形、五邊形……(圖1、2、3)。
 圖1
圖1 圖2
圖2 圖3
圖3每個圖形的點數分別稱為三角形數、四邊形數、五邊形數……除三角形數外,其餘的統稱多角形數(簡稱多角數),即滿足遞推關係
相關研究與結論
序號 | 邊數 n | 中間參數s=n-2 | 階數r |
1 | 2 | 3 | 4 | 5 | 6 | 7 | | r |
三角形 | 3 | 1 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | | |
四角形 | 4 | 2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | | |
五角形 | 5 | 3 | 1 | 5 | 12 | 22 | 35 | 51 | 70 | | |
六角形 | 6 | 4 | 1 | 6 | 15 | 28 | 45 | 66 | 91 | | |
七角形 | 7 | 5 | 1 | 7 | 18 | 34 | 55 | 81 | 112 | | |
八角形 | 8 | 6 | 1 | 8 | 21 | 40 | 65 | 96 | 133 | | |
| | | | | | | | | | | |
n角形 | n | n-2 | 1 | n | 3(n-1) | 2(3n-4) | 5(2n-3) | 3(5n-8) | 7(3n-5) | | |
…………
 圖4
圖4一般地,當
時,可得k角形數的數列為
從圖4可看出,從1開始連續奇數之和是一個平方數:
,做出平方數
後,再鑲上一個磬折形(亦稱曲尺形、拐尺形gnomon,此字來自伊奧尼亞學派)的邊,其中點數是
,就得出下一個平方數:
 圖5
圖5形數
稱為
磬折形數,又稱
曲尺形數、
拐尺形數等,用點子排出五角數和六角數,每邊點數為n(圖5),相應的磬折形(推廣)數是
和
,對三角數來說,磬折形(推廣,只是一條邊,對n階三角數,邊中點數是
)數是
。將磬折形數按所對應的多角數種類及多角數每邊點數排列起來形成磬折形數數列。三角數、四角數、五角數、六角數……的磬折形(推廣)數數列是:{2,3,4,5,…},{3,5,7,9,…},{4,7,10,13,…},{5,9,13,17,…},…,即分別由2,3,4,5,…開始,以1,2,3,4,…為公差的等差數列,n角數所對應的磬折形(推廣)數數列是
,其中
,因此,可計算出n角數的第r個數
,人們稱r為階數。上表是計算結果及公式,古希臘人已得出有關多角形數的一些定理(由幾何方法證明):
1.任一平方數都是二相繼三角形數之和,即
2.從1開始,任意n個從1開始的奇數之和是完全平方數,即
。
3.一個五角形數可表為同階四角形數與前一階三角形數之和:
。
4.首項為
,公差為
的等差數列
是
角形數的導出數列,稱為k階多角形數的導數列,導數列的公差為1,2,3,…,可分別導出三角數數列、四角數數列、五角數數列……導數列的公差為k時,可導出
角形數。
1636年,費馬(P.de.Fermat)提出:每一正整數可以用m個m階多角形數之和來表示,但未給出證明。1798年,勒讓德(A.-M.Legendre)證明了
的情形;1772年,拉格朗日(J.-L.Lagrange)證明了
的情形;1813年,柯西(A.-L.Cauchy)證明了一般情形。除了多角數外,畢達哥拉斯學派還研究了立方數、稜錐數(圖6)及形如
的長方數(圖7),並發現立方數與三角數有聯繫:從1開始的連續r個立方數之和必等於第r個三角數的平方,即
 圖6
圖6 圖7
圖7 圖1
圖1 圖2
圖2 圖3
圖3




































 圖4
圖4





 圖5
圖5
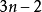



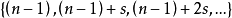


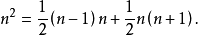




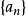



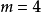


 圖6
圖6 圖7
圖7
