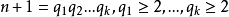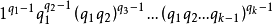完全分拆

完全分拆(perfect partition)是整數的一種分拆。若n∈N的一個分拆:n=k₁i₁+k₂i₂+...+k_si_s (1≤i₁<i₂<…<i_s，k₁≥1,...,k_s≥1)具有特性：對於任一正整數m<n，都有且只有一個形如:m=l_j1i_j1+...+l_jri_jr(1≤j₁<…<j_r≤s)，k_j1≥l_j1≥1,…，k_jr≥l_jr≥1的分拆，則此分拆稱為完全分拆。

基本介紹

• 中文名：完全分拆
• 外文名：perfect partition
• 所屬學科：數學（組合學）
• 簡介：整數的一種分拆

基本介紹

若n∈N的一個分拆：

，具有特性：對於任一正整數，都有且只有一個形如:

的分拆，則此分拆稱為完全分拆。正整數n的完全分拆

(即分拆有個1，個q₁，個q₁q₂，…，個)與n+1的有序因子分解之間可以建立一一對應關係，因而二者的個數相同。

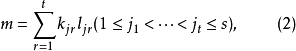
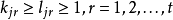
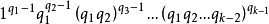
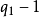
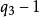
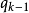
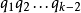
舉例與相關介紹

例如，n的分拆1ⁿ，即

就是一個完全分拆，又如，當n=7時，分拆41³，421，2³1和1⁷都是完全分拆。

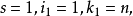
要想分拆(1)是一個完全分拆，必須至少有一個1-分部，否則1就不能表成(2)，故有，如果有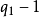個1-分部，那么，無小於q₁的非1分部存在是小於q₁的正整數的形如(2)的表法唯一的充要條件，如果這一條件滿足，則分拆必須至少有一個q₁-分部，否則q₁就不能表成(2)，故有i₂=q₁，如果有個q₁-分部，那么，無小於的非1且非q₁的分部存在是小於的正整數的形如(2)的表法唯一的充要條件，但是不能經前面的分部表出，因為前面的分部量的總和是

所以，繼續這種推理，必得n的分拆是

其中。

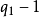
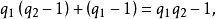
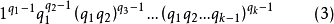
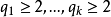
因而

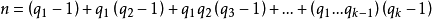
反之，如果n是形如(4)的數，則分拆(83)是一個完全分拆。這就證明了：

定理 正整數n+1的有序因子分解

與數n的完全分拆

之間的對應是(1一1)的，因而二者的個數相同。