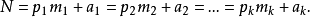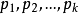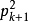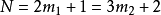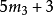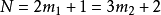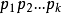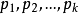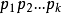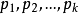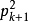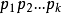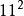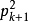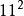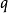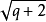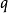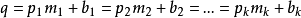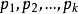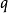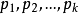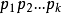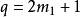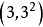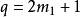公式
目錄
1、引言
2000多年前
歐幾里德在證明素數無窮多時就埋下了尋求素數普遍公式的伏筆,以
布勞維爾為首的直覺主義學派認為:“你沒有給出第n個素數是如何構造的,就不能算是好的證明”。2000多年來,數論學最重要的一個任務,就是尋找素數普遍公式,為此,一代又一代數學精英,耗費了巨大的心血,始終未獲成功。
黎曼曾想用他的ζ函式數的“零點”來逼近素數普遍公式,至今未獲成功。也有人反向思考,用素數普遍公式逼近“零點”來解決
黎曼猜想。
希爾伯特在1900年的
國際數學家大會上說:對黎曼公式進行了徹底討論之後,或許就能夠嚴格解決哥德巴赫問題和孿生素數問題。實際在哲學上,只要有一個明確的定義,就應該有一個公式。
 作者王曉明,在紐約哥倫比亞大學習
作者王曉明,在紐約哥倫比亞大學習2、素數普遍公式
(一)“要得到不大於某個自然數N的所有
素數,只要在2---N中將不大於
的素數的倍數全部划去即可”。
(二)將上面的內容等價轉換:“如果N是合數,則它有一個因子d滿足1<d≤
”。(《基礎數論》13頁,U杜德利著,上海科技出版社)。.
(三)再將(二)的內容等價轉換:“若自然數N不能被不大於
的任何素數整除,則N是一個素數”。見(代數學辭典[上海教育出版社]1985年。屜部貞世朗編。259頁)。
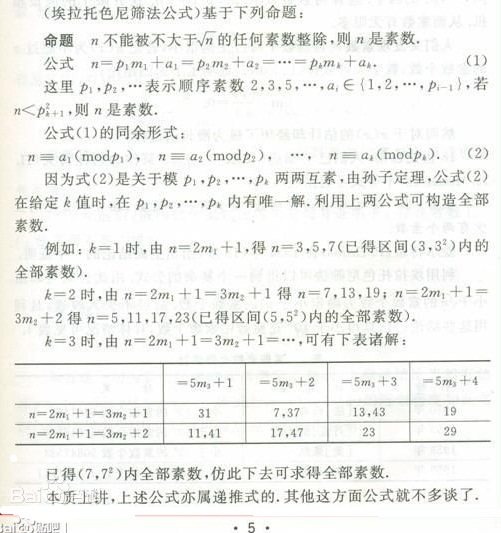
(四)這句話的漢字可以等價轉換成為用英文字母表達的公式:
...
(1)其中
表示順序素數2,3,5,,,,,。
。若
N<
,則
N是一個素數。
由於(2)的模
兩兩互素,根據
孫子定理(中國剩餘定理)知,(2)在
範圍內有唯一解。
例如k=1時,
,解得N=3,5,7。求得了(3,
)區間的全部素數。
k=2時,
,解得N=5,11,17,23。求得了(5,
)區間的全部素數。
k=3時 | | | | |
| 31 | 7; 37 | 13; 43 | 19 |
| 11; 41 | 17; 47 | 23 | 29 |
由孫子定理知,(1)式和(2)式在
範圍內有(2-1)(3-1)(5-1)....(
-1)個解。
兩式的本質是從
中除去pm(m〉1)的
合數,這一點與埃拉托塞
篩法不同,埃氏篩是用
去篩
以內的合數,剩下的就是
以內的素數了。
例如用2,3,5,去篩49以內的合數,剩下的就是(7,
)區間的素數了。但是,(1)(2)式是用
去篩
以內的pim(i≤k)形的數,連同模
也篩掉了。
切比雪夫證明了“
<
對於由4開始的所有的K 都是對的。例如,
>2,
>2×3,
>2×3×5,
<2×3×5×7。從11開始都是這樣了。(參見[數學欣賞]漢斯拉德海著220頁“數30的一個性質”北京出版社1981.6)所以,若K≥4時,(1)(2)式的計算結果只能取
以內的值才是素數。
仿此下去可以一個不漏地求得任意給定數以內的全部素數。求得了(11,
)區間的全部素數。 共有(2-1)×(3-1)×(5-1)×(7-1)=48個解。 小於11平方的解。
3,孿生素數問題
公式 孿生素數有一個十分精確的普遍公式,利用素數判定法則:“若自然數
與
都不能被不大於
的任何素數整除,則
與
是一對素數,稱為孿生素數。這一句話用數學語言表達就是:
上式可以用同餘式組表示:
由於(2)式的模
兩兩互素,根據孫子(中國剩餘)定理,對於給定的b值,(2)式在
範圍內有唯一的解。
4,範例
例如,k=1時,
,解得
=3和5,5<
,得知3與3+2,5與5+2是兩對孿生素數。從而得到了
區間的全部孿生素數。
k=2時,
=
。解得
=5,11,17。17<
,得知11與11+2,17與17+2是孿生素數對,從而得到
區間的全部孿生素數。
5,推論
孿生素數猜想就是要證明(4)式或者(5)式在k值任意大時都有小於
的解。
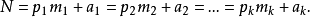
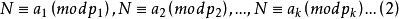
 作者王曉明,在紐約哥倫比亞大學習
作者王曉明,在紐約哥倫比亞大學習