基本介紹
- 中文名:同餘式
- 外文名:congruence
- 所屬學科:數學
- 表達式:a≡b(mod m)
基本概念
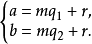
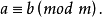
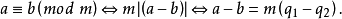
同餘式的性質
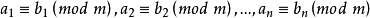
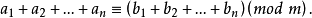
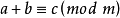
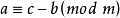
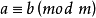
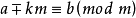
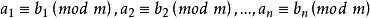
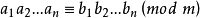
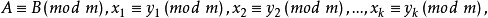
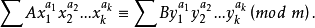
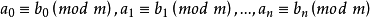
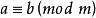
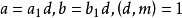
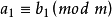
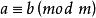
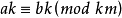
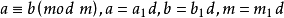
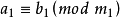
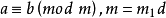
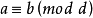
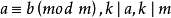
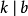
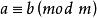
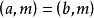
孫子剩餘定理
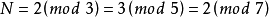
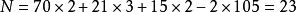
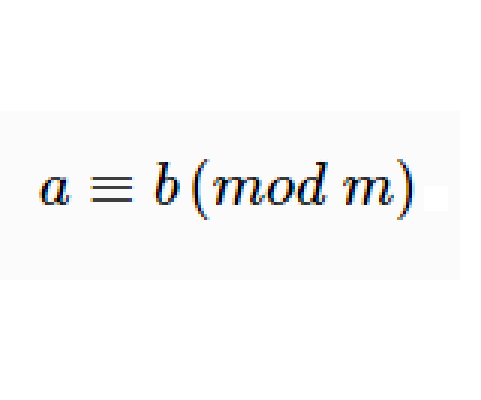
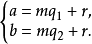
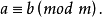
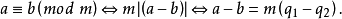
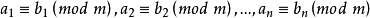
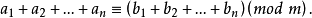
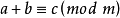
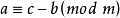
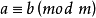
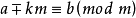
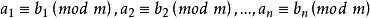
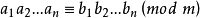
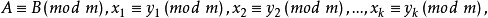
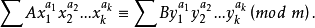
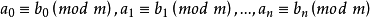
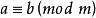
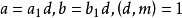
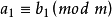
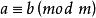
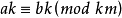
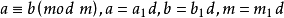
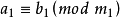
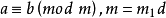
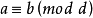
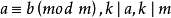
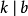
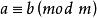
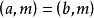
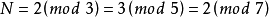
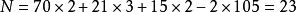
同餘式是數論的基本概念之一,設m是給定的一個正整數,a、b是整數,若滿足m|(a-b),則稱a與b對模m同餘,記為a≡b(mod m),或記為a≡b(m)。這個式子稱...
數論中的重要概念。給定一個正整數m,如果兩個整數a和b滿足a-b能夠被m整除,即(a-b)/m得到一個整數,那么就稱整數a與b對模m同餘,記作a≡b(mod m)。對模...
《同餘式及其套用》是2009年12月1日高等教育出版社出版的圖書,作者是徐誠浩。...... 《同餘式及其套用》用豐富的例子、通俗的語言、易懂的證明,介紹同餘式的概念...
重模同餘式(congruence with respect to double modulus)是同餘式的一種推廣,給定素數p和多項式φ(x),若f₁(x)-f₂(x)為φ(x)之倍式mod p,則稱f₁...
用指數表解同餘式(solving congruence withindex table)同餘式的一種解法。...... 用指數表解同餘式(solving congruence withindex table)同餘式的一種解法。...
一次同餘方程亦稱線性同餘方程,是一類簡單的同餘方程,指未知數僅出現一次冪的同餘方程。若a,b都是整數,m是正整數,當a≢0 (mod m)時,把ax=b (mod m)稱...
《同餘理論》是2012年5月哈爾濱工業大學出版社出版的圖書,作者是南秀全、劉漢文。本書較系統地介紹同餘的概念及其基本性質,解同餘式的理論和方法等內容。 ...
運用初等數論中的同餘運算產生均勻偽隨機數的一類數學方法的總稱,包括加同餘法、乘同餘法、混契約余法以及組契約余法等。同餘法,由於用同餘式做產生偽隨機數的遞推...
二項同餘方程(binomial congruence equation)亦稱二項同餘式,是一類特殊的同餘方程,設k≥1,同餘方程xk≡a(mod m),(a,m)=1被稱為是模m的二項同餘方程。...
用一常數與已產生的偽隨機數之積的同餘式做遞推公式,產生均勻偽隨機數的方法。 遞推公式為: 其中,a為乘子;c稱為增量;m稱為模;a、c和m均為非負整數。 ....
組合同餘法是指乘同餘法和混合同餘法組合產生均勻偽隨機數的一種方法。...... 組合同餘法是指乘同餘法和混合同餘法組合產生均勻偽隨機數的一種方法 [1] 。...
利用兩數之和的同餘式產生均勻偽隨機數的方法。 ...... 利用兩數之和的同餘式產生均勻偽隨機數的方法。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,...
線性同餘發生器(Linear congruential generator),簡稱LCG,是一種能產生具有不連續計算的偽隨機序列的分段線性方程的算法,它代表了最古老和最知名的偽隨機序列生成器...
秦九韶 數學1202~1247 創立解一次同餘式的“大 衍求一術”和求高次方程數值解的正負開方術 秦九韶—— 1202~1247 年,中國數學家。寫有《數書九章》,創立解...
《基層數論》是2011年3月1日哈爾濱工業大學出版社出版的圖書,作者是杜德利(美)。本書主要介紹了整數和同餘式等多種數論的基本概念和性質。...
《華羅庚文集:數論卷2》共二十章,前六章是屬於基礎知識,內容包括:整數分解、同餘式、二次剩餘、多項式之性質、素數分布概況、數論函式等;後十四章是就解析數論、...
1 同餘的定義和基本性質2 剩餘類和完全剩餘系3 縮系4 一次同餘式5 模數是素數的同餘式6 孫子剩餘定理及其套用舉例7 模數是素數冪的同餘式8 整數的剩餘表示...
