公約數
相關詞條
- 公約數
公約數,亦稱“公因數”。它是一個能被若干個整數同時均整除的整數。如果一個整數同時是幾個整數的約數,稱這個整數為它們的“公約數”;公約數中最大的稱為最大...
- 最大公約數
最大公因數,也稱最大公約數、最大公因子,指兩個或多個整數共有約數中最大的一個。a,b的最大公約數記為(a,b),同樣的,a,b,c的最大公約數記為(a,b,c...
- 約數
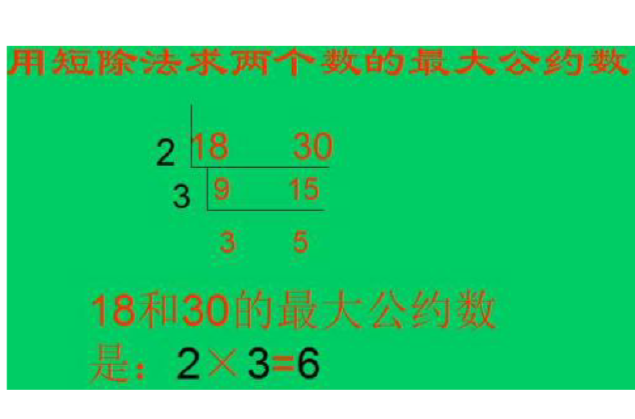
將需要求最大公因數的兩個數A,B分別分解質因數,再從中找出A、B公有的質因數,把這些公有的質因數相乘,即得A、B的最大公約數。...
- 價值觀“最大公約數”
習近平:確立價值觀“最大公約數”,關乎國家命運。...... 習近平:確立價值觀“最大公約數”,關乎國家命運。習近平:確立價值觀“最大公約數”,關乎國家命運。...
- 全社會意願和要求的最大公約數
習近平指出,在中國社會主義制度下,有事好商量,眾人的事情由眾人商量,找到全社會意願和要求的最大公約數,是人民民主的真諦。涉及人民利益的事情,要在人民內部商量好...
- 為改革尋求最大公約數
報告工作時稱,回顧過去一年,全國政協常委會的工作突出表現為四個方面,其中去年是全面深化改革的第一年,全國政協圍繞全面深化改革廣泛凝心聚力,尋找最大公約數、匯聚...
- 觀念的價值:尋求最大公約數
觀念的價值:尋求最大公約數內容簡介 編輯 《觀念的價值》主要講述一個年輕的創業者的心路歷程。作者提出了一個非常重要的觀點,人類文明的走向都與對信息的獲取有關...
- 素數公約數
套用介紹 這是一款可以計算素數和公約數的應用程式,軟體包含了: 1.素數, 2.素因數分解, 3.最大公約數, 4.最低公倍數。 ...
- 全面建成小康社會:凝聚全民最大公約數
《全面建成小康社會:凝聚全民最大公約數》為2017年黨建讀物出版社出版的圖書,作者是陳寶生。...
- 正約數
約數:如果一個整數能被兩個整數整除,那么這兩個數就是這個數的約數。約數是有限的,一般用最大公約數。所有數都有約數1.例:15能被3整除,我們就說15是3的倍數...
- 公因數
公因數,亦稱“公約數”。它是一個能被若干個整數同時均整除的整數。如果一個整數同時是幾個整數的因數,稱這個整數為它們的“公因數”;公因數中最大的稱為最大...
- 最大公因數
最大公因數,也稱最大公約數,指兩個或多個整數共有約數中最大的一個。a,b的最大公約數記為(a,b)。求最大公約數有多種方法,常見的有質因數分解法、輾轉相...
- 九章算術
另外還系統地講述了分數的四則運算法則,以及求分子分母最大公約數等方法。第二章“粟米”:穀物糧食的按比例折換;提出比例算法,稱為今有術;衰分章提出比例分配...
- 數學名詞
四捨五入法 純循環小數 一次二項式 二次三項式 最大公約數最低公倍數 代入消元法 加減消元法 平方差公式 立方差公式立方和公式 提公因式法 分組分解法 十字...
- 質因數
所分出的質因數無疑都能整除原數,因此這些質因數也都是原數的約數。從分解的結果看,12與18都有公約數2和3,而它們的乘積2×3=6,就是 12與18的最大公約數...
- 輾轉相除法
輾轉相除法, 又名歐幾里德算法(Euclidean algorithm),是求最大公約數的一種方法。它的具體做法是:用較大數除以較小數,再用出現的餘數(第一餘數)去除除數,再用...
