基本介紹
- 中文名:同餘定理
- 外文名:Congruence theorem
- 屬性:數學概念
- 記法:a≡b(mod d)
- 性質:反身性、對稱性、傳遞性等
- 相關定理:歐拉定理、費馬小定理、孫子定理
理論背景
同餘符號
定義
證明
性質






相關定理
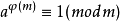




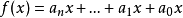







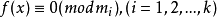

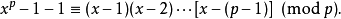







同餘一般指本詞條






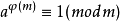




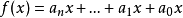







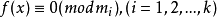

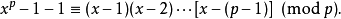






數論中的重要概念。給定一個正整數m,如果兩個整數a和b滿足a-b能夠被m整除,即(a-b)/m得到一個整數,那么就稱整數a與b對模m同餘,記作a≡b(mod m)。對模...
同餘式是數論的基本概念之一,設m是給定的一個正整數,a、b是整數,若滿足m|(a-b),則稱a與b對模m同餘,記為a≡b(mod m),或記為a≡b(m)。這個式子稱...
數論中的重要概念。給定一個正整數m,如果兩個整數a和b滿足a-b能夠被m整除,即(a-b)/m得到一個整數,那么就稱整數a與b對模m同餘,記作a≡b(mod m)。對模...
運用初等數論中的同餘運算產生均勻偽隨機數的一類數學方法的總稱,包括加同餘法、乘同餘法、混合同餘法以及組合同餘法等。同餘法,由於用同餘式做產生偽隨機數的遞推...
同餘的基本性質(fundamental properties of con-gruences)同餘理論的重要內容之一關於同餘的基本性質。...
用一常數與已產生的偽隨機數之積的同餘式做遞推公式,產生均勻偽隨機數的方法。 遞推公式為: 其中,a為乘子;c稱為增量;m稱為模;a、c和m均為非負整數。 ....
同餘方程是一個數學方程式。該方程式的內容為:對於一組整數Z,Z里的每一個數都除以同一個數m,得到的餘數可以為0,1,2,...m-1,共m種。我們就以餘數的大小...
同餘關係是代數系統的集合中的等價關係,並且在運算的作用下,能夠保持關係的等價類。以二元運算為例,在a₁*a₂中,如果用集合S中與a₁等價的任何其他元素b...
MOD,同餘符號,在數學上,兩個整數除以同一個整數,若得相同餘數,則二整數同餘(英文:Modular arithmetic;德文:Kongruenz)。同餘理論常被用於數論中。最先引用同餘的...
一次同餘方程亦稱線性同餘方程,是一類簡單的同餘方程,指未知數僅出現一次冪的同餘方程。若a,b都是整數,m是正整數,當a≢0 (mod m)時,把ax=b (mod m)稱...
數論中,線性同餘方程是最基本的同餘方程,“線性”表示方程的未知數次數是一次...... 數論中,線性同餘方程是最基本的同餘方程,“線性”表示方程的未知數次數是一次....
恆等同餘(identity congruence)是兩個多項式之間的一種等價關係,指相應係數都分別對模p同餘的兩個多項式。設p為素數,f(x),g(x)為整係數多項式,若f(x)-g(x)...
《同餘理論》是2012年5月哈爾濱工業大學出版社出版的圖書,作者是南秀全、劉漢文。本書較系統地介紹同餘的概念及其基本性質,解同餘式的理論和方法等內容。 ...
數學上,同餘(英語:congruence modulo,符號:≡)是數論中的一種等價關係。當兩個整數除以同一個正整數,若得相同餘數,則二整數同餘。同餘是抽象代數中的同餘關係的...
一次同餘方程組是一類簡單的同餘方程組,指形如x≡bi(mod mi) (i=1,2,…,k)的同餘方程構成的組。k=2是最簡單的一次同餘方程組,指x≡bi(mod mi) (i=1...
同餘對(congruence pair)用於刻畫逆半群上同餘的一個重要概念.設S是一逆半群,E是它的冪等元半格,K是S的一個正規子半群,即K是S的逆子半群,且EcK,對任意...
同餘記號是一個數學名詞,兩個整數a,b,如果它們除以自然數m所得的餘數相等,則稱a,b對於模m同餘。...
組合同餘法是指乘同餘法和混合同餘法組合產生均勻偽隨機數的一種方法。...... 組合同餘法是指乘同餘法和混合同餘法組合產生均勻偽隨機數的一種方法 [1] 。...
《同餘式及其套用》是2009年12月1日高等教育出版社出版的圖書,作者是徐誠浩。...... 《同餘式及其套用》用豐富的例子、通俗的語言、易懂的證明,介紹同餘式的概念...
同餘科技團隊成立於2013年初,致力於智慧型設備安全領域,依託強大的技術團隊,為國內外知名職能設備廠商提供安全解決方案及配套產品。 北京同餘科技有限公司,在APP套用和...
5 同餘符號 6 八卦乾卦 7 電腦打法 ≡全等於號 編輯 (is equivalent to) 如果△ABC全等於△A'B'C',那么可表示為△ABC≡△A'B'C'(也可表示為“≌...
孫子定理是中國古代求解一次同餘式組(見同餘)的方法。是數論中一個重要定理。又稱中國餘數定理。一元線性同餘方程組問題最早可見於中國南北朝時期(公元5世紀)的數學...
數論倒數(number-theoretic reciprocal)亦稱算術倒數,是與同餘有關的一個基本概念。設m為模,a為任意整數,且(a,m)=1。若有整數a′能滿足同餘式a′a≡1(mod ...
