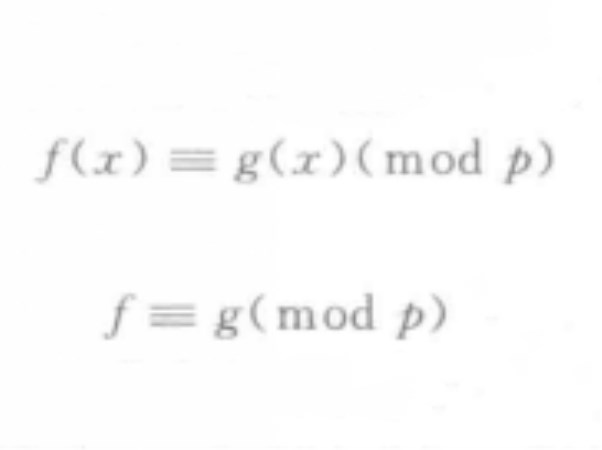恆等同餘

恆等同餘(identity congruence)是兩個多項式之間的一種等價關係，指相應係數都分別對模p同餘的兩個多項式。設p為素數，f(x)，g(x)為整係數多項式，若f(x)-g(x)的各項係數全被p整除，則稱f(x)，g(x)對素數模p恆等同餘，記為f(x)≡g(x)(mod p)或f≡g(mod p)。

基本介紹

• 中文名：恆等同餘
• 外文名：identity congruence
• 所屬學科：數學
• 所屬問題：初等數論(多項式的性質)
• 簡介：兩個多項式之間的一種等價關係

基本介紹

設f(x)，g(x)為整係數多項式，p為素數，若多項式f(x)-g(x)的所有係數均能被p整除，則稱f(x)與g(x)對模p恆等同餘，記為f(x)≡_xg(x)(mod p)或f(x)≡g(x)(mod p)，或簡記為f≡_xg(p)，並稱此關係式為模p的恆等同餘式。

注意，對所有x均有f(x)≡g(x)(mod p)，並不一定能推出f(x)≡_xg(x)(mod p)，例如x^p-x≡0(mod p)和x²+x≡0(mod 2)對一切x均成立，但x^p-x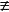_x0(mod p)，x²+x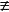_x0(mod 2)。反之，若f(x)≡_xg(x)(mod p)，則必有f(x)≡g(x)(mod p)對一切x成立。

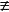
恆等同餘的性質

恆等同餘有下述性質：

1.f(x)≡_xf(x)(mod p)。

2.f(x)≡_xg(x)(mod p)的充分必要條件是

g(x)≡_xf(x)(mod p)。

3.若f(x)≡_xg(x)(mod p)，

g(x)≡_xh(x)(mod p)，

則f(x)≡_xh(x)(mod p)。

4.若f₁(x)≡_xg₁(x)(mod p)，

f₂(x)≡_xg₂(x)(mod p)，

則f₁(x)±f₂(x)≡_xg₁(x)±g₂(x)(mod p)，

f₁(x)f₂(x)≡_xg₁(x)g₂(x)(mod p)，

特別重要的有(f(x))≡_xf(x)(mod p)。