基本介紹
- 中文名:整係數多項式
- 外文名:polynomial with integer coefficients
- 所屬領域:數論
- 定義:各項係數都是整數的多項式
定義
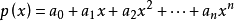

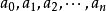

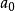

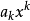

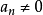
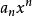

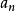




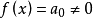

相關性質
定理1

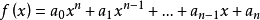
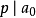
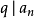

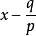


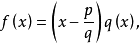
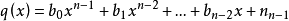


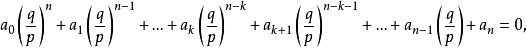
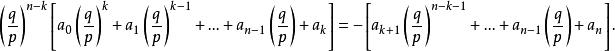

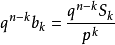
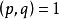
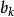
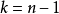
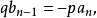
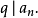
推論1
推論2



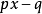
定理2



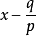
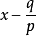



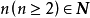
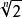
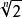
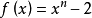
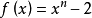
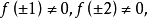

定理3

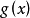

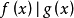

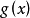

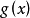
推論3

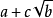
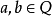
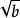
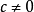
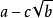

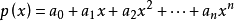

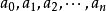

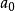

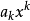

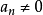
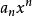

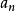




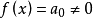


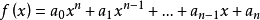
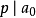
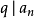

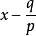


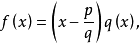
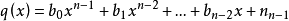


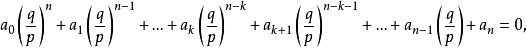
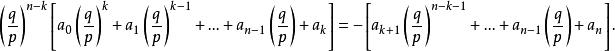

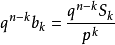
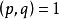
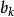
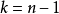
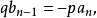
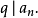



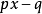



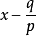
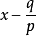



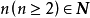
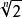
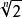
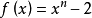
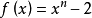
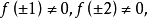


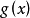

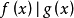

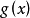

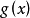

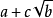
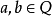
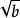
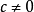
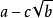
整係數多項式是數論中研究的一類多項式,指係數都是整數的多項式。所有的整係數多項式對加、減、乘運算是自封閉的。如果一組整係數多項式適合以下條件時,就稱這組整...
兩個本原多項式的乘積是本原多項式。套用高斯引理可證,如果一個整係數多項式可以分解為兩個次數較低的有理係數多項式的乘積,那么它一定可以分解為兩個整係數多項式...
有理係數多項式是高等代數裡面多項式因式分解討論的一個特例。我們知道,每個次數大於等於1的有理係數多項式都能惟一地分解成不可約的有理係數多項式的乘積。但是對於...
高斯引理在代數(特別是環理論),如果一個整係數多項式的所有係數是互素的,則稱它是一個本原多項式,本原多項式對判定不可約多項式有很大幫助,高次多項式的不可約...
亞歷山大多項式(Alexander polynomial)扭結型的比扭結群更加易於計算的不變數。在數學中,亞歷山大多項式是一個結不變數,它為每個結類型分配一個具有整數係數的多項式。...
整係數多項式f(x)除以(x-a)商為q(x),餘式為r,則 。如果多項式r=0,那么多項式f(x)必定含有因式(x-a)。反過來,如果f(x)含有因式(x-a),那么,r=0。...
),找出一元多項式 的一次因式的關鍵是求多項式 的根.對於任意多項式 ,要求出它的根是沒有一般方法的,然而當多項式f(x)的係數都是整數時,即整係數多項式時,若既...
代數數是代數與數論中的重要概念,指任何整係數多項式的復根。所有代數數的集合構成一個域,稱為代數數域。不是代數數的實數稱為超越數,例如圓周率。...
一個整係數的n次多項式anx + an − 1x + ...a1x + a0,若px − q是f(x)之因式,且a,b互質,則:(逆敘述並不真)a −...
高斯引理(Gauss lemma )多項式理論的主要命題之一即任意兩個本原多項式的乘積仍是一個本原多項式。 [1] 由高斯引理可知,任一非零的整係數多項式如果能夠分解為兩...
任意交換的帶單位元的環 R 的元素 a 稱為整數環 Z 上的整元,簡稱整元。如果 a 是一個首一的整係數多項式的零點,R的所有整元構成一個帶單位元的子環。...
