定義
證明

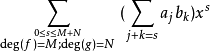
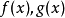
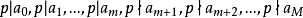

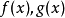
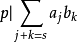
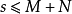




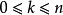
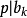
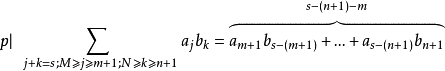
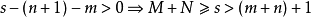

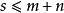
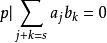
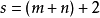
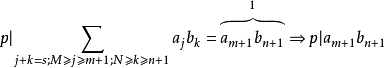
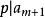


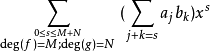
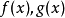
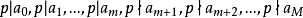

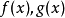
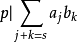
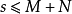




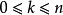
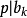
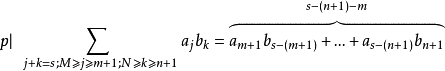
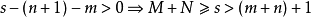

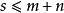
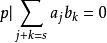
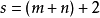
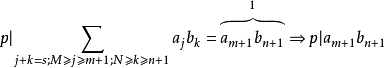
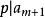

多項式的高斯引理是數論和高等代數中的一條引理,是揭示本原多項式性質的結果。指出:多個本原多項式之乘積本原。...
高斯引理(Gauss lemma )多項式理論的主要命題之一即任意兩個本原多項式的乘積仍是一個本原多項式。 [1] 由高斯引理可知,任一非零的整係數多項式如果能夠分解為兩...
高斯引理:本原多項式的乘積還是本原多項式。證明:設 和 分別是n次與m次的本原多項式。令其中這裡,當s>n或t>m時,規定 及 。假定 不是本原的,則存在 上的...
兩個本原多項式的乘積是本原多項式。套用高斯引理可證,如果一個整係數多項式可以分解為兩個次數較低的有理係數多項式的乘積,那么它一定可以分解為兩個整係數多項式...
有理係數多項式定理1(高斯(Guass)引理) 編輯 兩個本原多項式的乘積還是本原多項式。有理係數多項式定理2 編輯 如果一個非零的整係數多項式能夠分解成兩個次數較低...
高斯引理:本原多項式的乘積還是本原多項式。參考資料 1. 丁昶欣. 可分生成域擴張的生成元[J]. 中國科學院大學學報, 2009, 26(01):18-22. 2. 丘維聲. ...
有理根定理是高斯引理對多項式因式分解的特殊情況(單線性因子)。 如果導數係數 ,則整數根定理是有理根定理的特殊情況。 [1] 有理根定理套用 編輯 為了確定一個...
高斯引理(環的)兩個本原多項式的乘積仍是本原多項式。線性反饋移位暫存器流密碼 編輯 流密碼是私鑰密碼體制的一類流密碼與分組密碼用固定變換處理明文序列的一組...
8.2.2 復係數多項式的因式分解8.2.3 實係數多項式的因式分解8.2.4 多項式的零點和係數的關係8.3 有理係數多項式8.3.1 高斯引理...
看成是整係數多項式。根據高斯引理亦可假設該多項式的未知因式是整係數多項式 [1] 。如果 是可約的整係數多項式,則存在有 和 ,使恆等式 成立。不失討論的一般性...
4. 多項式函式、餘數定理、多項式的根及性質. 5.代數基本定理、復係數與實係數多項式的因式分解. 6. 本原多項式、Gauss引理、有理係數多項式的因式分解、Eisenstein...
