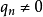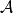代數數

代數數是代數與數論中的重要概念，指任何整係數多項式的復根。

所有代數數的集合構成一個域，稱為代數數域。

不是代數數的實數稱為超越數，例如圓周率。

基本介紹

• 中文名：代數數
• 外文名：Algebraic number
• 相關術語：代數數域
• 定義：任何整係數多項式的復根
• 套用學科：數學
• 所屬領域：代數與數論

定義

形如（，n為正整數）的整係數（為整數，）代數方程的根x則叫做“代數數”。

代數數可以定義為“有理係數多項式的復根”或“整係數多項式的復根”。第一個定義可以具體描述為：

設z為複數。如果存在正整數n，以及n+ 1個有理數，並且，使得：

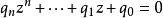
則稱z是一個代數數。

這個定義中，由於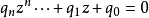可以推出，其中整數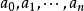分別等於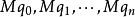，M是n+ 1個有理數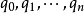分母的最低公倍數。所以“存在有理係數多項式使得z是其復根”可以推出“存在整係數多項式使得z是其復根”。另一方面，由於整數集合是有理數集合的子集，所以“存在整係數多項式使得z是其復根”也可以推出“存在有理係數多項式使得z是其復根”。這說明兩個定義是等價的。

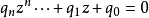
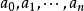
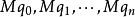
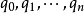
例子

例如√2是一個實代數數，它滿足方程x²-2=0 。再如全體有理數及i (虛數單位，)等都是代數數。

每個有理數都是代數數，因為它滿足方程 nx-m= 0（m,n為整數 ，n≠0）。

每個高斯整數都是代數數，所謂高斯整數，是形如a+bi的複數，其中a和b都是整數。因為a+bi是方程(x²-a²+b²)²+4a²b²=0的複數解。

同理，實部和虛部都是代數數的複數也是代數數。

當a是有理數時，sin aπ、cos aπ、tan aπ、e^aπi等也是代數數。

所有規矩數（即可以從單位長度的線段出發，通過尺規作圖法做出的線段的長度數值）都是代數數。因為建立直角坐標系後可以證明，標準的尺規作圖步驟的每一步都相當於計算一個次數不超過2的多項式方程，因此能夠通過有限步做出的線段長度必然是有限個有理係數多項式疊代後得到的多項式的根，從而是代數數。

自然對數的底e和圓周率π都不是代數數。

性質

代數數在有理數下的“+”、“-”、“x”、“÷”運算中是封閉的，因此構成一個域，稱為代數數域。

注意：代數數在平方和開方的運算中不是封閉的，例如2^(√2)，即2的根號2次方不是代數數，它是一個超越數。

以代數數作為係數的有限次多項式的根也是代數數。

當a為一個非零代數數時，sin a、cos a、tan a、e^a都是超越數。當a為一個大於0且不等於1的代數數時，ln a是超越數。

代數數域

兩個代數數的和、差、積與商（約定除數不為零）也是代數數。可以驗證，裝備了有理數的加法、乘法運算的代數數集合構成一個域，有時也記為。每一個係數為代數數的多項式方程的根也是代數數。因此，代數數域是代數封閉域。實際上，它是含有有理數域的最小的代數封閉域，稱為有理數域的代數閉包。

代數整數

代數整數是任何整係數首一多項式的根。顯然代數整數是代數數的一部分，但代數數不全是代數整數。所有整數都是代數整數，其餘的有理數則不是代數整數。代數整數的集合記作A，是代數數的子集。在某些上下文中，為了與代數整數區別，整數也被稱作有理整數。

兩個代數整數的和、差與積也是代數整數，這就是說，裝備了整數的加法、乘法運算的代數整數集合構成了一個環，因此A代數中也被稱為代數整數環。

與實數集關係

代數數集包含了有理數集。然而，代數數集並不包含全部實數。代數數集是一個可數集，即所有代數數能與全體自然數建立一一對應，而實數集是不可數的無窮集，因此，一定存在不是代數數的實數。現已證明 π和e這些無理數不是代數數，但不是所有的無理數都不是代數數。不是代數數的數稱為超越數。由此可見，就實數集而言，實數既可按有理數和無理數分為兩類，又可按實代數數和實超越數分為兩類。實代數數集是有理數集的自然擴充。