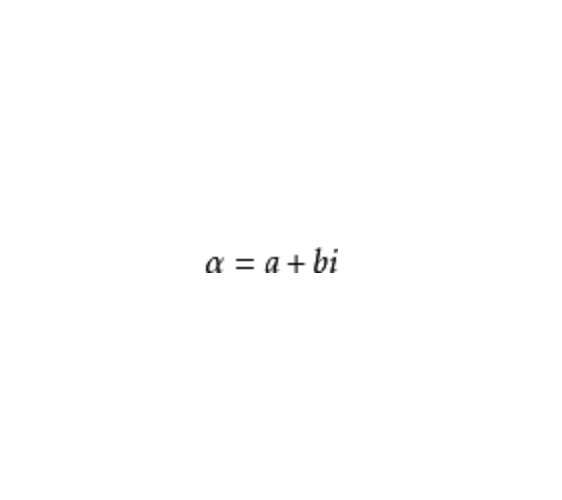基本介紹
簡介,性質,加、減、乘運算,整除性,高斯素數,
簡介
數論的一個重要分支——代數數論把整數的一些理論推廣到了一些特殊的代數整數集合。所謂代數整數就是首一(首項係數是1)整係數多項式的根。而高斯整數即是一類特殊的代數整數集合。
形如  (其中a,b是整數)的複數被稱為高斯整數,高斯整數全體記作Z[i]。注意到若 γ=a+bi 是高斯整數,則它是滿足如下方程的代數整數
(其中a,b是整數)的複數被稱為高斯整數,高斯整數全體記作Z[i]。注意到若 γ=a+bi 是高斯整數,則它是滿足如下方程的代數整數


性質
通常我們使用希臘字母來表示高斯整數,例如α,β,γ和δ。注意到若 n 是一個整數,則 n=n+0i 也是高斯整數。當我們討論高斯整數的時候,把通常的整數稱為有理整數。
加、減、乘運算
高斯整數在加、減、乘運算下是封閉的,正如下面定理所述。
定理1:設 α=x+iy 和 β=w+iz 是高斯整數,其中 x,y,w 和 z 是有理整數,則 α+β,α-β 和 αβ 都是高斯整數。
雖然高斯整數在加、減和乘運算下封閉,但是他們在除法運算下並不封閉,這一點與有理整數類似。此外,若 α=a+bi 是高斯整數,則 N(α)=a2+b2 是非負有理整數。
整除性
我們可以像研究有理整數那樣去研究高斯整數。整數的許多基本性質可以直接類推到高斯整數上。要討論高斯整數的這些性質,我們需要介紹高斯整數類似於通常整數的一些概念。特別地,我們需要說明一個高斯整數整除另一個高斯整數的意義,並給出高斯素數的定義。
定義1:設 α 和 β 是高斯整數,我們稱α整除β,是指存在一個高斯整數 γ 使得β=αγ。若α整除β,我們記作α|β ;若α 不整除β ,記作α β 。
β 。

高斯整數的整除也滿足有理整數整除的一些相同的性質。例如,若α,β和γ 是高斯整數,α|β,β|γ,則α|γ。再者,若α,β,γ,ν和μ 是高斯整數,γ|μ,γ|β,則γ|(μα+νβ)。